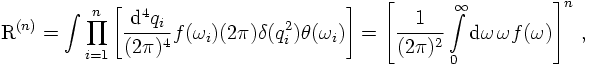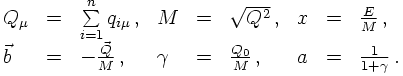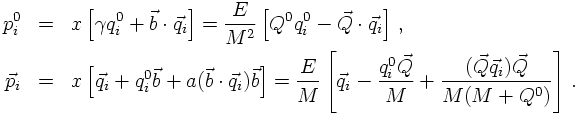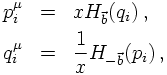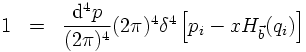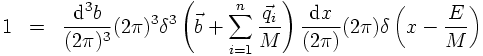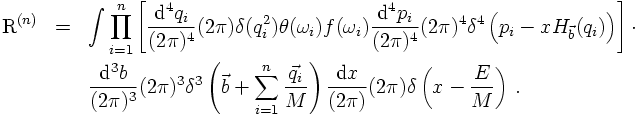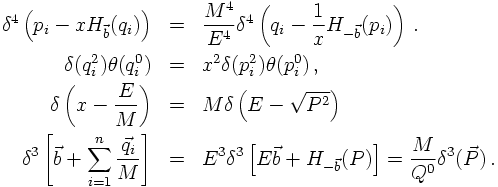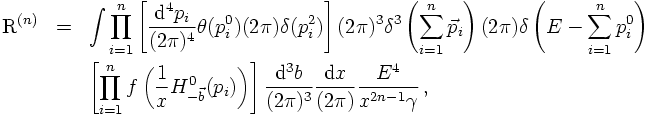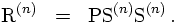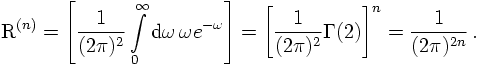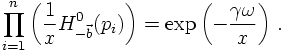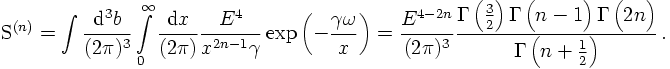Three and more particles
RAMBO FOR MASSLESS PARTICLES
Consider the phase space volume of an n particle final state produced in a process
with c.m. momentum P and corresponding energy E. It is given by
 Instead of calculating it directly, let's take a detour first and discuss the direct
way of evaluating an n-particle phase space at another moment. For the detour, consider the
unconstrained n-particle phase space R first. There, the δ-function implementing
four-momentum conservation is replaced with some damping function f, acting on the
individual particle energies. To make the difference between constrained and unconstrained
momenta apparent, in the following the unconstrained momenta are denoted by q and their
energies are denoted by ω. However, unconstraining the momenta by replacing the
four-momentum conservation with a damping function, effectively decouples the
four-momenta and results in
Instead of calculating it directly, let's take a detour first and discuss the direct
way of evaluating an n-particle phase space at another moment. For the detour, consider the
unconstrained n-particle phase space R first. There, the δ-function implementing
four-momentum conservation is replaced with some damping function f, acting on the
individual particle energies. To make the difference between constrained and unconstrained
momenta apparent, in the following the unconstrained momenta are denoted by q and their
energies are denoted by ω. However, unconstraining the momenta by replacing the
four-momentum conservation with a damping function, effectively decouples the
four-momenta and results in
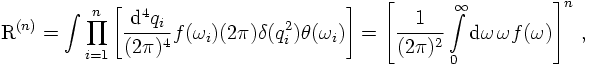 where the factor 2π stems from the integration over the solid angle of each three-momentum
after going to spherical coordinates. If the function f(ω) is going to 0 fast enough for
large energies, this integral will be finite.
where the factor 2π stems from the integration over the solid angle of each three-momentum
after going to spherical coordinates. If the function f(ω) is going to 0 fast enough for
large energies, this integral will be finite.
To link the constrained and the unconstrained four-momenta, a conformal transformation
(a combination of Lorentz boost and rescaling) has to be performed. Introducing
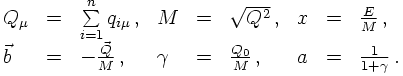 With these quantities the relation of the p and the q reads
With these quantities the relation of the p and the q reads
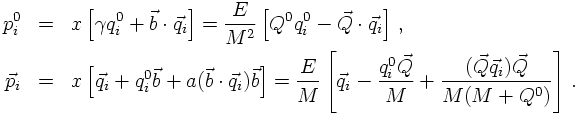 This transformation and its inverse can be cast into
This transformation and its inverse can be cast into
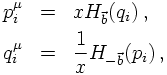 making explicit the role of the boost vector b and the scale factor x.
Adding in two intelligent factors of one, namely
making explicit the role of the boost vector b and the scale factor x.
Adding in two intelligent factors of one, namely
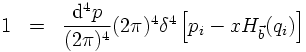 and
and
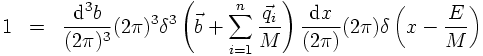 allows to cast R into the following form:
allows to cast R into the following form:
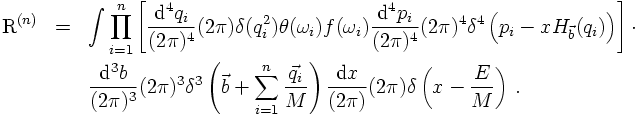 This allows to eliminate the unconstrained momenta q. To do so, the δ-functions
have to be written in a more suitable form. Simple properties of the δ-function
imply that
This allows to eliminate the unconstrained momenta q. To do so, the δ-functions
have to be written in a more suitable form. Simple properties of the δ-function
imply that
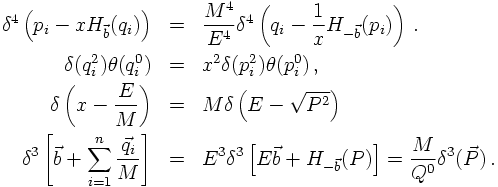 This allows to perform the q integrations yielding
This allows to perform the q integrations yielding
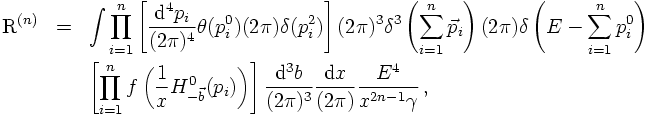 where the first line looks surprisingly identical to the original phase space integral.
Therefore, the unconstrained phase space integral and the constrained one are connected
through a function S, which depends on the form of f that has been chosen.
where the first line looks surprisingly identical to the original phase space integral.
Therefore, the unconstrained phase space integral and the constrained one are connected
through a function S, which depends on the form of f that has been chosen.
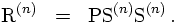
CHOOSING F
There is a simple choice for f allowing to calculate both R and S, namely f(x)=exp(-x).
In this case, the equation for R becomes
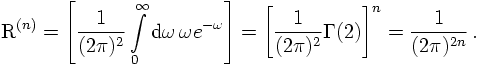 On the other hand, S is given by the "extra piece" in the unconstrained phase space
incorporating the conformal transformation. Emplying that P is already in its c.m.
system and therefore looks like
On the other hand, S is given by the "extra piece" in the unconstrained phase space
incorporating the conformal transformation. Emplying that P is already in its c.m.
system and therefore looks like
 leads to
leads to
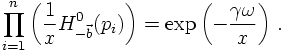 Changing integration variables in S from x and b to Eγ/x and 1/γ² finally
results in
Changing integration variables in S from x and b to Eγ/x and 1/γ² finally
results in
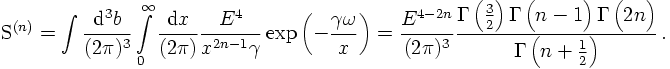 Employing the properties of the Γ-function yields the actual phase space volume of n
massless particles having total energy E. It reads
Employing the properties of the Γ-function yields the actual phase space volume of n
massless particles having total energy E. It reads
 Plugging in numbers for n, i.e. setting n=2 and n=3, actually reproduces the results
obtained before.
Plugging in numbers for n, i.e. setting n=2 and n=3, actually reproduces the results
obtained before.