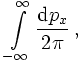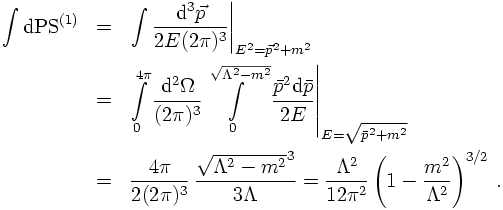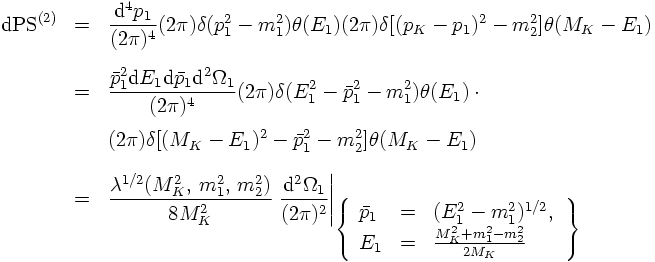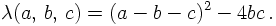One- and two-particle phase space
ONE-PARTICLE PHASE SPACE: LORENTZ INVARIANCE
Let's return to a discussion of the concept of phase space.
When particles are produced in a reaction, they must move somewhere.
Assuming that a reaction takes place at the origin of a spatio-temporal
coordinate system, the particle's trajectories are fully defined by their
momenta when leaving the reaction zone. Their future propagation and
eventual decays are subject to quantum mechanics. It is also clear
that the probability for any reaction to happen is proportional to the
number of states the final state of this reaction can reach. This, of course,
also includes all possible momentum states a particle is allowed to have.
But, how many such states exist? Since momentum is continous, the result
will be an integral over such states; in one dimension, say px
this is nothing but
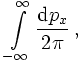 where a normalisation of 2π has conveniently been added. To keep such
an integral Lorentz-invariant, all four dimensions have to be integrated over.
But this won't be enough, after all, physical particles obey a mass-shell
relation. This relation can be implemented through a δ-function, again
with a suitable normalisation. In addition, physical particles do have
positive energies, this requirement is induced by a step function. Taken
together, the phase space cell for one momentum state therefore is given by
where a normalisation of 2π has conveniently been added. To keep such
an integral Lorentz-invariant, all four dimensions have to be integrated over.
But this won't be enough, after all, physical particles obey a mass-shell
relation. This relation can be implemented through a δ-function, again
with a suitable normalisation. In addition, physical particles do have
positive energies, this requirement is induced by a step function. Taken
together, the phase space cell for one momentum state therefore is given by
 It is interesting to note that the first line clearly is manifest Lorentz-invariant,
whereas te last one hides this a little bit.
It is interesting to note that the first line clearly is manifest Lorentz-invariant,
whereas te last one hides this a little bit.
ONE-PARTICLE PHASE SPACE: VOLUME
But, how large is the phase space of a particle when its energy has to be smaller
than, say, some constant Λ ? To see this, the integral actually has to be
performed. This is done best by going to spherical coordinates for the three-momentum.
The solid angle (two-dimensional) is denoted by Ω, its integral is given by the
surface of a sphere with radius one, 4π. Therefore the full integral over the
phase space results in
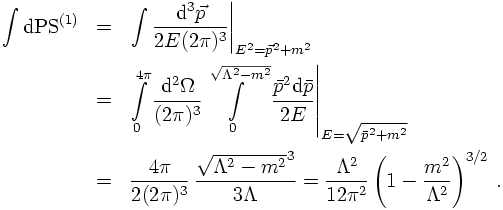 As could be anticipated, the phase space grows quadratically with the energy. This
is not too large of a surprise, after all, the volume of a sphere in n dimensions
(here, n=3) goes with its radius to the n-th power. Here, this is reduced by the
term 1/E, reducing the growth to a quadratic growth.
As could be anticipated, the phase space grows quadratically with the energy. This
is not too large of a surprise, after all, the volume of a sphere in n dimensions
(here, n=3) goes with its radius to the n-th power. Here, this is reduced by the
term 1/E, reducing the growth to a quadratic growth.
TWO-PARTICLE PHASE SPACE: ADDING IN FOUR_MOMENTUM CONSERVATION
The discussion of the one-particle phase space can now be extended to the case of two
particles produced in a reaction. As an illustrative example, consider the case of a
binary decay, like the decay of a kaon into two pions, K→ππ. To keep things
simple, it is useful to choose the kaon's rest frame. In this frame, the kaon
four-momentum is given by
 The phase space of the two outgoing pions is given by the product of both
individual phase spaces times a factor, taking care of four-momentum conservation.
In full generality this factor can be written as a δ-function, again
with proper normalisation. It reads
The phase space of the two outgoing pions is given by the product of both
individual phase spaces times a factor, taking care of four-momentum conservation.
In full generality this factor can be written as a δ-function, again
with proper normalisation. It reads
 where the sums go over all incoming (i) or ourgoing (o) particles. The second expression
shows the specialisation of the first, general one to the simple examplatory
case of K →ππ. The total two-particle phase space thus reads
where the sums go over all incoming (i) or ourgoing (o) particles. The second expression
shows the specialisation of the first, general one to the simple examplatory
case of K →ππ. The total two-particle phase space thus reads
 where the total four-momentum conservation has been used to carry out the
phase space integral of one particle (here, it's particle 2). This can be done
for every number of final state particles: The phase space integral for one of them
can be used to eliminate the four-momentum conservation. In order to continue,
the integral over the three-momentum of particle 1 can be cast into spherical
coordinates. Then the integral over both the energy and the size of the three-momentum
of particle 1 can be carried out through the δ-functions,
where the total four-momentum conservation has been used to carry out the
phase space integral of one particle (here, it's particle 2). This can be done
for every number of final state particles: The phase space integral for one of them
can be used to eliminate the four-momentum conservation. In order to continue,
the integral over the three-momentum of particle 1 can be cast into spherical
coordinates. Then the integral over both the energy and the size of the three-momentum
of particle 1 can be carried out through the δ-functions,
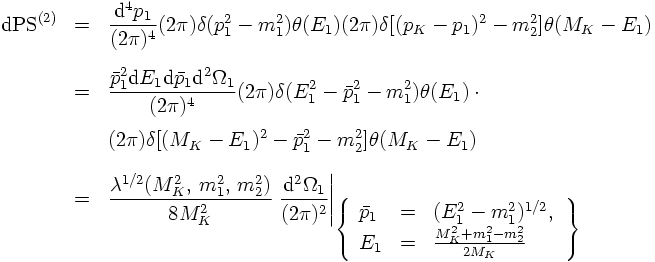 The function λ(a,b,c) is a function typical for phase space integrations. It
reads
The function λ(a,b,c) is a function typical for phase space integrations. It
reads
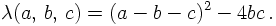 The total two-particle phase space integral above therefore can be reduced to
the integral over the solid angle of particle 1 in the rest frame of the decaying
particle. For massless decay products, the total phase space available thus is
just
The total two-particle phase space integral above therefore can be reduced to
the integral over the solid angle of particle 1 in the rest frame of the decaying
particle. For massless decay products, the total phase space available thus is
just
 In any case, such a two-body phase space, when integrated over a constant number,
is just a number in itself. For decays without any prefered direction, the function
to be integrated over is constant w.r.t. θ and φ, and the corresponding width
related to the decay can thus be more or less read off.
In any case, such a two-body phase space, when integrated over a constant number,
is just a number in itself. For decays without any prefered direction, the function
to be integrated over is constant w.r.t. θ and φ, and the corresponding width
related to the decay can thus be more or less read off.