Basics

Phase spacing

1. One- and two-particle phase space
   
2. Three and more particles
   
3. MC Integration: Sampling
   
4. Smarter sampling methods
   
5. Selection according to a distribution: Unweighting
   

   WHAT IS UNWEIGHTING?

   Having integrated a cross section with the methods similar to the ones discussed so far, there is a second, related way of using Monte Carlo methods in particle physics, namely for simulation purposes. Simulation there in most cases translates into generating individual events (including detector simulation etc.) as they would be finally observable, according to a probability distribution which reflects the best knowledge of the physics responsible for the observations. In principle there is an easy cook-book recipe for perfomring such a simulation: Just pick a sufficient set of random numbers, pass them through the p.d.f. of your simulation and read of the result. Then fill the histograms etc. accordingly with the value of the combined p.d.f.. This simple recipe, however, is not very efficient in most cases, since usually with this recipe a plethora of events with tiny weights (probabilities from the p.d.f.) would be generated and only few events with a sizable impact on histograms etc.. Therefore, rather than generating and accepting events with varying probability, it has become custom to generate events with relative weight equal to one - unweighted events. The probability for events in certain regions of phase space/parameter space in such a case is then directly related to the number of events in this region.
   
   

   ANALYTIC UNWEIGHTING ALGORITHM

   Unweighting can also be understood as the process of selecting random numbers according to a p.d.f., a problem that has been already encountered. If the integral of the p.d.f. f(s) exists in the range from s_min to s_max, and if it can be inverted, then:
   
   • Generate a uniformly distributed random number R in the interval [0,1],
   • compare it with the ratio of integrated f(s). Solve for s in the equation below
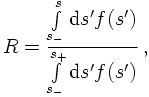
   • the various s will be distributed according to f(s).
   This algorithm can be tried out here.
   
   However, in most realistic cases, the p.d.f. is just not simple enough but rather a complicated function, which is in many cases not even known analytically. Then, of course, analytic integration and inversion are just completely out of the question and different methods have to be invoked. They will be discusseed below.
   
   
6. Unweighting: Hit-or-miss
   
7. Problems