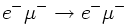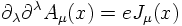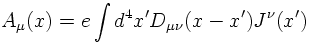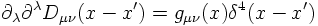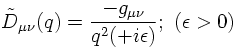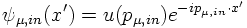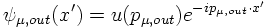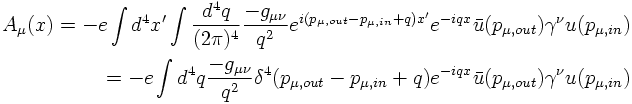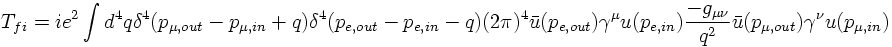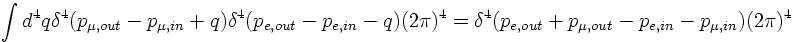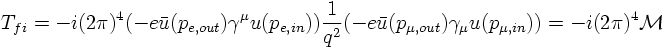QED

Feynman Graphs

1. Interaction of an electron with an external electromagnetic field
   
2. Electron Muon scattering
   To calculate the transition amplitude for an electron scattered on a muon 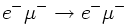one calculates the potential A_μ generated by the transition current (density) of the scattered muon J_μ.
   The potential A_μ generated by the current density J_μ fulfills the differential equation 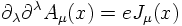A solution for A_μ is given by 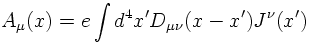where D_μν is the Greens function solving the equation 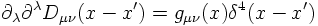Again, the solution is easily found by a Fourier transformation: 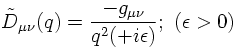which is called the photon propagator for a photon with four-momentum q.
   
   
   THE FOUR-POTENTIAL GENERATED BY THE SCATTERED MUON
   
   With these ingredients one can calculate the four-potential generated by the scattered muon for an incoming muon described by 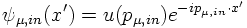and an outgoing muon described by 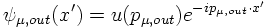The four-potential is 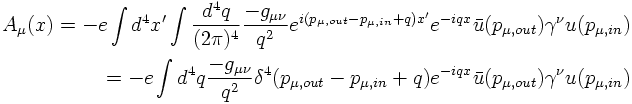With corresponding electron wave functions the transition amplitude is given by 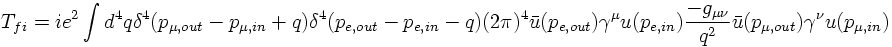where one has to integrate over the four-momentum q of the virtual photon:
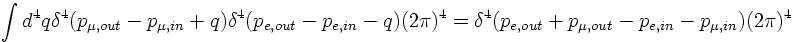
   From the general consideration of the S-matrix one identifies the T-matrix element for electron-muon scattering to first order:
   
   
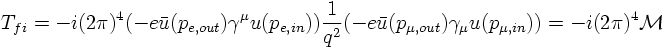
3. The Feynman Rules