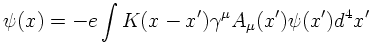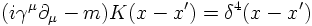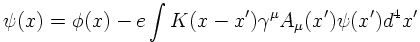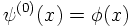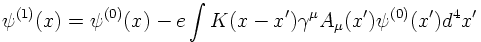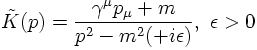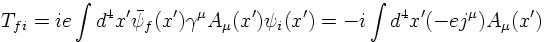QED
Feynman Graphs
- Interaction of an electron with an external electromagnetic field
The E.o.M. for a charged Dirac particle interacting with an external electromagnetic field is
given by the inhomogenous Dirac equation
The E.o.M. is solved by
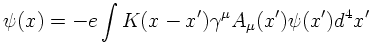where K(x-x') is the Greens function solving
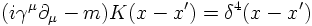The solution for ψ(x) is an integral equation which contains ψ!
The idea is to solve it in an iterative way by expanding the solution
in a perturbation series of the (small) coupling constant (charge) e.
Each term in this expansion can be visualized by a Feynman graph.
Writing the general solution as a sum of the solution for the homogenous
Dirac equation, φ(x), and for the inhomogenous Dirac equation, respectively,
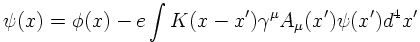the solution to zeroth order is
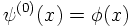The solution to first order is
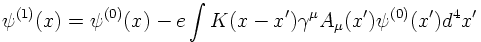and so on.
The solution to first (second) order corresponds to a single (double) scattering
on the external potential.
The Greens function K(x-x') can be found by going to the Fourier space.
The solution for the electron propagator is:
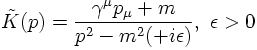The transition amplitude for an initial plane wave ψi(x)
going into a final plane wave ψf(x) to first order is then
given by
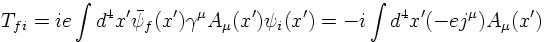
- Electron Muon scattering
- The Feynman Rules