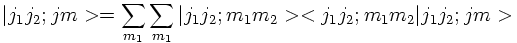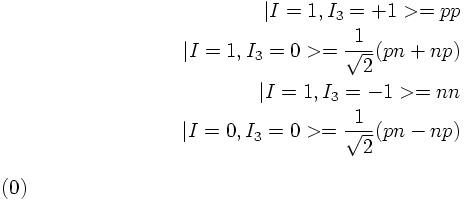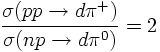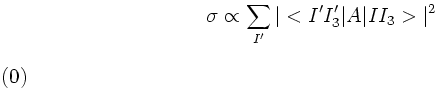The Dirac Equation

Introducing Spin

1. The Stern-Gerlach experiment
   
2. Spin vs. orbital angular momentum
   
3. Connection to the Pauli-matrices
   
4. Fields with internal degrees of freedom: Isospin and Colour
   
5. Example of isospin conservation
   
   ADDITION OF (ISO)SPINS
   When adding two angular momenta or (iso)spins J₁ and J₂, J = J₁ + J₂, one can express the states |j₁,j₂;j m> in terms of the basis |j₁,j₂; m₁,m₂>: 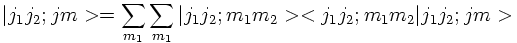where < j₁,j₂; m₁,m₂|j₁,j₂;j m> are the Clebsch-Gordan coefficients.
   The Clebsch-Gordan coefficients for several combinations can be found here: PDG homepage: Clebsch-Gordan coefficients.
   
   For a system of two nucleons the isospin states expressed in terms of the nucleon isospins are given by
   
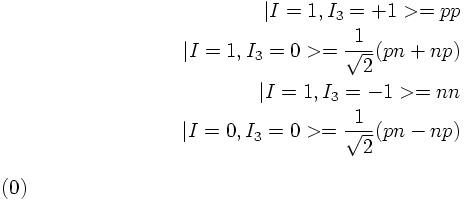
   EXAMPLE FOR ISOSPIN CONSERVATION
   If isospin is conserved in strong interactions one can predict e.g. the following ratio of cross sesctions 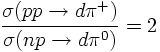If one neglects the slightly different masses between the neutrons and protons, and charged and neutral pions, respectively, the cross sections are just given by isospin amplitudes squared: 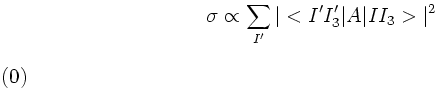With I(d)=0 and I(π)=1 and using isospin conservation the ratio is predicted to be equal to 2.
6.