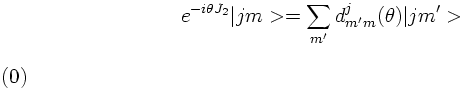The Dirac Equation

Introducing spin

1. The Stern-Gerlach experiment
   
2. Spin vs. orbital angular momentum
   The operators S_x, S_y and S_z fulfill Hence, these operators have the properties of an angular momentum.
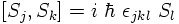
   The electron spin can not be an orbital angular momentum though since the quantum mechanical analogon to the classical orbital angular momentum has only eigenvalues: where n is an integer.
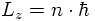
   As a consequence, it has to be a new-type internal degree of freedom.
   Compared to orbital angular momenta spin 1/2 is special concerning a rotation of a spinor state around an axis by an angle θ. E.g. when considering a rotation around the 2-axis one has for a general angular momentum J ket |j m>: The rotation matrices are tabulated e.g. here: PDG homepage: rotation matrices. Hence, for spin 1/2 the system is rotated by θ/2!
3. Connection to the Pauli-matrices
   
4. Fields with internal degrees of freedom: Isospin and Colour
   
5. Example of isospin conservation
   
6.