In the following two additional examples of internal degrees of freedom are discussed which play an important role in particle physics: ISOSPIN and COLOUR.
ISOSPIN
It is striking that the hadrons, proton and neutron, have both almost equal mass: mp=938.27 MeV, mn=939.57 MeV.
This observation lead to the concept of ISOSPIN (introduced by Heisenberg). Like two electrons, one with spin 'up' and the other with spin 'down' are considered as one particle with the internal degree of freedom 'spin', a proton and a neutron are considered as one particle, called nucleon with an additional internal degree of freedom called isospin.
In this formalism the proton is a NUCLEON with isospin I=1/2 and the third component being I3=+1/2 whereas the neutron is a nucleon with isospin I=1/2 and the third component being I3=-1/2 or in short
|p>=|1/2,+1/2> , |n>=|1/2,-1/2>.
These correspond to the spinors |+> and |->.
The concept of isospin is very useful because the strong interaction conserves isospin:
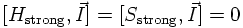
Hence, the strong interaction does not distinguish between a proton (p) and a neutron (n). This is known as CHARGE INDEPENDENCE of strong interaction: The p-p interaction, the n-n interaction and the n-p interaction are of equal strength as far as the strong interaction part of the Hamiltonian is concerned. Of course charge independence is not exact since the electromagnetic interaction distinguishes a neutron from a proton due to their different electric charges. This is in analogy to the Stern-Gerlach experiment where the two spin states of the electron can be distinguished due to the external magnetic field.
It should be noted that in reality the strong interaction Hamiltonian is not exactly invariant under a rotation in the isospin state: the isospin symmetry is only an approximate symmetry and accidental in the following sense:
Neutrons and protons are not elementary particles but can be considered as being composite particles built up by three quarks: (qqq).
In this picture the proton is a bound (uud)-system and the neutron is a (udd)-system where |u>=|1/2,+1/2> , |d>=|1/2,-1/2>.
The similar masses of protons and neutrons are caused by the fact that u quarks and d quarks have similar masses. The strong interaction does not distinguish between the quark flavor u and d. However, since the quark flavors u and d have slightly different masses there is a breaking of this flavor symmetry in strong interactions. As a consequence, the nearly equal masses of u and d quarks lead to a nearly perfect isospin symmetry. Hence, the concept of isospin allows a useful classification of strong interaction processes due to the fact that u and d quarks have (by accident ?) almost equal masses.
As it will be seen later on the generation of the quark masses in the Standard Model is provided by the Higgs mechanism. Within the Standard Model the mass values are just parameters the numerical values of which are not predicted by the theory. Even if there is a theory beyond the Standard Model which eventually will explain these mass values the concept of isospin is nothing more than just a very efficient way of classifying strong interaction processes.
COLOUR
The fundamental symmetry of strong interaction is related to the internal degree of freedom called 'COLOUR'. Each quark carries a 'charge' with three different possible values called 'red', 'green' and 'blue'. The fundamental symmetry of strong interactions is the invariance of the strong Hamiltonian under a rotation in the three-dimensional 'Colour' space.
The existence of the internal degree of freedom 'Colour' is not just a theoretical construct! It is well motivated by experimental facts as will be shown later on.