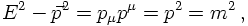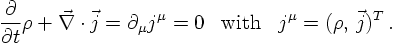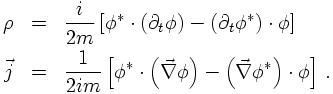Relativistic formulation:
The Klein-Gordon equation
INCLUDING RELATIVISTIC INVARIANCE
If relativistic invariance is to be combined with quantum mechanics,
a relativistic analogon of the Schrödinger equation needs to be constructed.
In the relativistic case, the energy-momentum relation reads
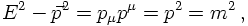where from now on again Plancks constant and the speed of light have been set
to one, thereby fixing the system of units. Using the correspondence
principle the resulting Klein-Gordon equation reads
where the short-hand notation
has been employed.
CONTINUITY EQUATION
Let us try to formulate again a continuity equation. Written in relativistic
invariant form, it reads
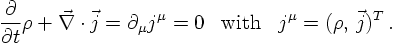After a bit of algebra it turns out that
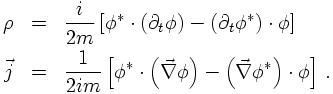The bad news here, is that ρ is not positive definite, hence it cannot be considered
as probability density for the particles. In contrast, it could well be interpreted
as a charge density (which does not need to be positive). Another problem also arises,
namely the fact that when this field is expanded in terms of plane waves, the quadratic
dependence on the energy in the equation of motion above allows for solutions with
negative energies. Clearly, as long as
there's no obvious contradiction with the relativistic description, and the negative energy
solutions appear on the same footing as the positive ones. In this case, the physical spectrum
of states is not bound from below any longer. Pictorially, this means that any state could decay
into another one with smaller energy. In other words, it seems as if any amount of energy, even
arbitrarily large, may be extracted from the system. When Dirac looked into this, he
considered these problems to be so overwhelming that he worked on introducing another equation,
capable of describing relativistic particles in the framework of quantum mechanics. However,
for the time being, let's just ignore these problems and continue with an attempt to
create a quantised theory out of the Klein-Gordon equation.