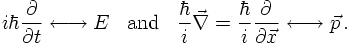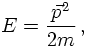The Dirac Equation

Schrödinger and Klein-Gordon equation

1. Non-relativistic quantum mechanics: The Schrödinger equation
   

   QUANTUM MECHANICAL FORMULATION IN BRIEF

   In quantum mechanics, the states of a system are represented by bra's <ψ| and ket's |ψ>, which are normalised vectors in a Hilbert space H. The absolute value squared of a scalar product of such vectors, |<ψ|ψ>|², denotes the probability of finding the system in the state ψ. Physical observables are identified with Hermitian operators Â, acting on the Hilbert space H. Measurements, if performed often enough, yield the expectation value <ψ|Â|ψ> of the operator, if the system is in the state ψ. The time evolution of the system is governed by the Schrödinger equation, where H denotes the (self-adjoint, i.e. Hermitian) Hamiltonian of the system. From this, the time evolution operator Û can be constructed. It is defined through and therefore satisfies
   
   

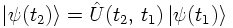
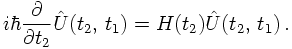
   SCHRÖDINGER EQUATION FOR FREE PARTICLES

   Let us now discuss briefly the Schrödinger equation for free particles. To do so, it is convenient to move to the usual configuration space. There, the operators containing derivatives w.r.t. time and position can be associated with the energy and the three-momentum, repsectively, i.e. Since for a free, massive particle, the energy-momentum relation is given by the Schrödinger equation reads In this form, it describes nonrelativistic, massive free particles. These particles have a density ρ, which satisfies the following continuity equation Clearly, the density ρ is positive definite, hence it can be interpreted as a probability density, with j the corresponding probability flux. In its integral form, this continuity equation therefore connects the temporal change of particle number inside a volume with a flux of particles through its surface.
   
   
2. Relativistic formulation: The Klein-Gordon equation
   
3. Equations of motion and quantisation
   
4. Equations for a complex scalar field
   
5.