VEGAS IN GENERAL
When information about the function to be integrated is not available, the preference clearly is on adaptive techniques, i.e. on algorithms that learn about the function when integrating them. Vegas, which will be discussed here is a prime example for such an adaptive Monte Carlo algorithm; it automatically concentrates on those regions of the integrand where it is largest.Vegas starts by dividing the n-dimensional hypercube [0,1]n into smaller ones - usually of identical size - and performs a sampling in each of them. The results are then used to refine the integration grid for the next iteration of the sampling procedure. The refinement is done by approximating the optimal p.d.f. p of the function f,

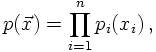
However, the nice thing about Vegas is that the evaluation of an integral can be divided into two phases: Firstly, the grid is initialised and optimised with many iterations and comparably few sampling points, and only then the "true" sampling leading to a result starts with comparably many sampling points distributed over the now frozen grid. In each iteration j, the estimator and the variance are calculated afresh, based on the sampling points of this iteration only,


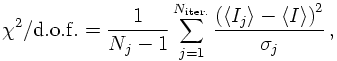
WEIGHTS IN VEGAS: THE P.D.F.'s AND THEIR EVOLUTION
In fact, a closer look into the algorithm reveals that instead of reweighting the bins in each iteration step, their boundaries are shifted. This is done in the following way (for simplicity, scetched for one dimension only): The first iteration starts out with a fixed number Nbins of bins, each of which having the same size Δxi= 1/Nbins.After the first iteration, each bin i is subdivided into mi bins according to its contribution <Ii> to the total estimator,
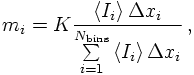

In so doing, however, the binning and rebinning may lead to oscillations in the grid which destabilise the convergence. to avoid them, a damping term may be included into the evaluation of the mi, for example
