Detector

Interaction of charged particles with matter

1. Interaction of charged particles with matter
   Charged particles are losing energy and are deflected when traversing matter. The following effects are responsible for these effects:
   
   * INELASTIC COLLISIONS WITH ATOMIC ELECTRONS
   This process leads to energy loss of charged particles. The mean energy loss per path length (in MeV g^-1 cm²) is provided by the Bethe-Bloch formula: where K = 0.307 MeV mol^-1 cm²; z(e) is the charge of the particle and β is its velocity; Z and A (in g mol^-1) are the atomic number and atomic weight of the material, respectively; T_max is the maximum kinetic energy transfer in a single collision; I is the mean excitation potential and δ is called the density correction caused by the fact that the electric field of the particle polarizes the material and hence causes a shielding of the particle's electric field.
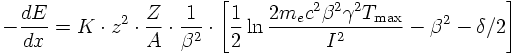
   * The maximum energy transfer is given by * For electrons T_max is different due to the identical nature of the particles.
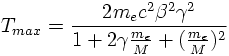
   * The minimum of the mean energy loss takes place close to βγ=4.
   * It may happen that the energy transfer in a collision is so large that the recoil electrons give rise to secondary ionizations ('δ-electrons')!
   * For a thin absorber the p.d.f describing the energy loss can be approximated by a 'Landau distribution'.
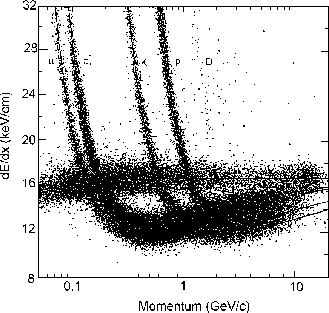
   The following example (D. R. Nygren, J. N. Marx, Physics Today 31 (1978) 46) shows an average of 185 energy deposition measurements in the PEP4/9-Time Projection Chamber (TPC).
   
   * ELASTIC SCATTERING FROM NUCLEI
   This effect leads to a deflection of the charged particle from its incident direction. For a very thin absorber material the deflection angle is given by the Rutherford formula.
   For a thick absorber multiple Coulomb scattering occurs.
   As there is a small probability of a very large scattering angle the distribution in the deflection angle is only a Gaussian for small scattering angles.
   If the momentum of the particle is small multiple scattering becomes important, i.e. the deflection angle may become so large that the precision of the track reconstruction e.g. using a drift chamber device is significantly influenced by multiple scattering.
   
   * EMISSION OF CHERENKOV PHOTONS
   If the particle velocity is larger than the speed of light inside the material Cherenkov radiation is emitted the emission angle of which with respect to the particle direction is given by where β is the velocity of the particle and n is the refraction index.
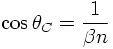
   The number of Cherenkov photons emitted per unit path length and per unit wavelength is given by the following formula: The energy loss due to emission of Cherenkov photons is small compared to the energy loss induced by inelastic collisions with atomic electrons.
   
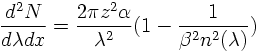
   * NUCLEAR REACTIONS
   Strongly interacting particles like protons, charged pions or charged kaons can interact with nuclei in the detector material by nuclear interactions. In case of inelastic interactions the particle will be absorbed inside the material.
   
   
   * BREMSSTRAHLUNG
   Light charged particles as electrons and positrons also loose energy by emission of Bremsstrahlung photons in the electric field of a nucleus.
   
   The emission probability (cross section) is proportional to the inverse square of the particle mass: m_e^-2.
   As a consequence, energy loss due to bremsstrahlung is 40000 times smaller for muons compared to electrons.
   
   The bremsstrahlung cross section is also proportional to Z²α³.
   
   Finally, the differential bremsstrahlung cross section dσ/dν as a function of the frequency ν is proportional to ν^-1.
   
   Above a critical energy, E_c, the energy loss due to bremsstrahlung supercedes the energy loss due inelastic collisions.
   An approximate formula is given by
   
   
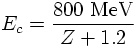
   The radiation length X₀ is characteristic for a material under consideration: It gives the path length after which the original electron energy E₀ is lowered by a factor of exp(-1). In other words: The radiation length is given by where r_e is the classical electron radius, α is the electromagnetic coupling constant, N₀ the Avogadro number and Z and A (in g mol^-1) are the atomic number and atomic weight of the material.
   
   
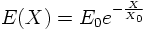
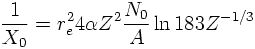
   SUMMARY: Energy Loss of charged particles
   e^+-: Bremsstrahlung, Bethe-Bloch
   μ^+-: Bethe-Bloch (-> penetrating characteristics)
   π,K,p: Bethe-Bloch, Hadronic interactions
   
   
   
2. Interaction of neutral particles with matter
3. A typical detector
4. Problems