Phase Transitions

Correlations

In the previous graph of energy vs. temperature, the energy per spin became less negative under the randomising effect of temperature. It would be expected that the energy becomes zero at temperatures above T_c, since there is no net magnetic moment, and therefore equal amounts of 'spin up' and 'spin down'. However, after the occurence of the phase change at \( T_c \), the energy per spin still remained negative. This suggests that there is still some residual alignment with the spins and their neighbours even as temperatures become much greater than \(T_c \). This is what we define as correlations. This occurs because the randomising effect of temperature is not strong enough to create a completely random alignment between neighbouring spins.

Correlation Function

In order to quantify the residual alignment of the spins, an initial spin is selected, and labelled s₀. The correlation function is found between the initial spin and a second spin, s_i, which is i lattice sites away from s₀. This correlation finction, f(i), is then calculated through the equation \( f(i)=\langle s_0 s_i \rangle \). In a Monte Carlo simulation, every spin is used as an s₀, and the correlation function is determined for all other spins. This ensures that all pairs of spins are investigated, over many time steps. This way the average of the product can be best evaluated.
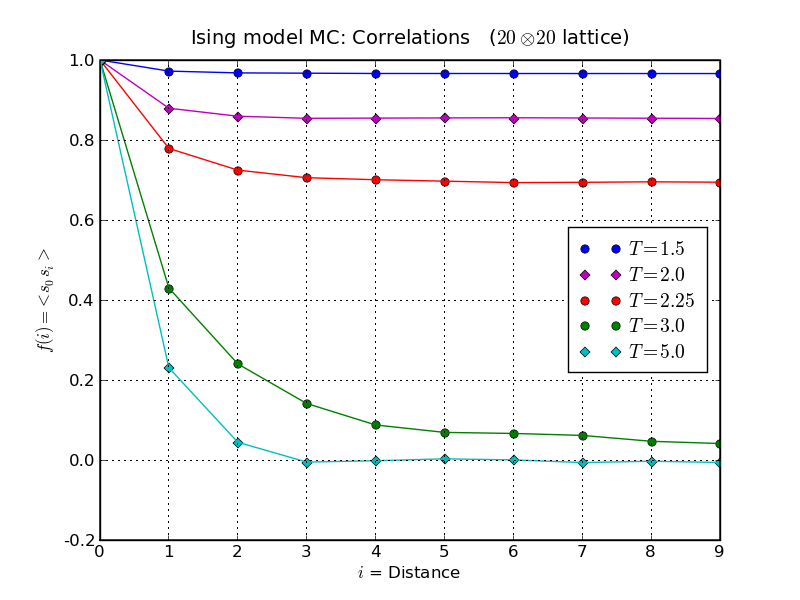
These are the results for the correlation function for a 20 × 20 lattice plotted at different temperatures.

At the low temperatures, the correlation function remains close to one: \(f(i) \approx 1\) for \(T\approx 0\). This shows that for low temperatures, the spin alignment is almost independant of the distance separating two spins. The correlation of neighbouring spins is measured as the increased alignment over short distances from the average shown in the system. There is therefore weak correlation in a short range for low temperatures. This changes around the critical temperature, T_C=2.27, where the alignment between spins is significantly stronger over short distances than it is over long distances. However, the alignments are still present at the larger distances. Once we get above T_c, the correlation function drops off incredibly rapidly after very short distances.

This behaviour of the correlation function can be further described at large distances from the central spin as exponential decay,

\[ f(i) \sim C_1 + C_2 \exp(-r_i/ \xi )\,\, . \]

ξ is the correlation length, a measure of the range over which the correlations of spin-fluctuations, (s-⟨s⟩), approach zero.
As the separation between two spins, r_i, tends to infinity, s₀ and s_i become uncorrelated. Therefore the product of the average values of the two spins is equal to the average value of the entire system squared, ⟨s⟩². The correlation function therefore becomes

\[ f(i) \longrightarrow \langle s_0 \rangle \langle s_i \rangle = \langle s \rangle ^2 \,\, . \]

As this is taken in the limit \(r_i \longrightarrow \infty \), it can also shown by comparison that C₁=⟨s⟩².
This allows us to rearrange to obtain

\[ f(i)-C_1 =\langle (s_0-\langle s \rangle)(s_i-\langle s \rangle) \rangle \sim C_2 \exp(-r_i/\xi) \,\, . \]

From the results for the correlation function at varying temperatures, it can be seen that ξ is a function of temperature.
In the limit of large lattices, ξ can be seen to diverge at T_c according to the power law,

\[ \xi \sim \frac{1}{|T-T_C|^\nu}\,\, , \]

with the critical exponent ν.
When T=T_c, ξ becomes infinite. This infinite correlation length means that all of the spins in the system are sensitive to every other spin. At this point of infinite ξ, the correlations alter as a power law function of the distance, r_i.

We have shown that while the total magnetic moment of a system at a temperature above T_c is zero, there is still some correlation between neighbouring spins. This leads us to the conclusion that the average alignment of near neighbours is different from the average alignment of the entire system. This effect is not taken into account in mean field theory, which completely ignores local fluctuations and therefore does not give an accurate description of the system at temperatures around T_c.

Frank Krauss and Daniel Maitre

Last modified: Tue Oct 3 14:43:58 BST 2017