Percolation
←Previous
Cluster labelling
The trick for checking for the emergence of a spanning cluster, implemented in
form of a computer code, will in fact rely on filling the lattice and labelling
clusters while doing so, rather than filling the lattice first and only then
trying to figure out what happened. While the former may result in tedious
but straightforward algorithms (see below), the latter essentially boils down
to an exercise in pattern recognition - nothing we want to do, if we can
avoid it.
Therefore, in all cases, the algorithm builds on sequentially filling a lattice
with single occupancies at random locations, starting from an empty lattice.
This process is stopped once a spanning cluster emerges. The occupancy at that
moment obviously equals p. In each step, i.e. for each lattice site being
occupied, a unique cluster number is attached to the site, and cluster numbers
are updated, once a site connects to hitherto unconnected clusters.
This would boil down to a first algorithm:
Main program
In the main program, the steering unit, the following tasks will
have to be fulfilled:
- Begin with an empty lattice, all sites labelled by '0'.
- Pick a site at random, label it with '1' (it's the first site, hence
the first cluster - so we label clusters with consecutive numbers).
- Repeat step 2 until a spanning cluster has emerged and pick a site
at random. Check whether any of its neighbours is already occupied:
- If no: Label this site with a new cluster number.
- If yes: Call this a bridging site and treat it accordingly (see
below).
- If a spanning cluster appeared, the current occupancy p of the
lattice equals the critical occupation probability
pc.
|
Bridging sites
Having picked a bridging site, check the neighbouring cluster numbers.
- If there is only one cluster number, the bridging site will get the
same number, i.e. it will just be added to the existing cluster.
- If there is more than one cluster number, the smallest of their
labels is picked, the bridging site will get the same number. Then
all clusters joined by the bridging site are relabeled with this new number,
such that the merged cluster again has an unique number.
|
Check for spanning clusters
If a site at the edge of the lattice is picked, this site will
be added to a list of "edge sites" in each cluster. This list will
at most comprise one site on each edge, if four sites are in this list,
the cluster is a spanning cluster.
This list needs to be updated in cluster mergings.
|
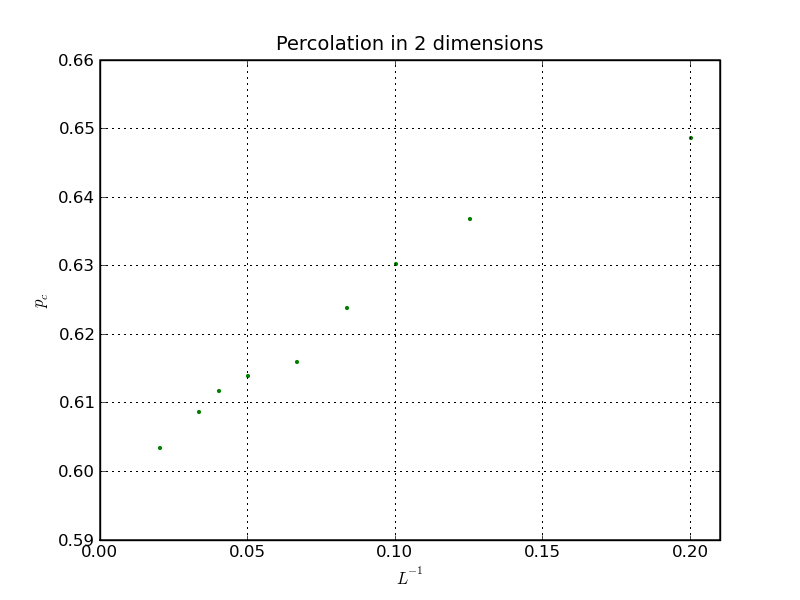
Below you see some results obtained with this algorithm for a square lattice of size L. For each
lattice size L, pc has been obtained from filling
50 L percolation lattices. Obviously there are some statistical
fluctuations visible in the plot. A linear fit in the left region is in
accordance with the known value of pc=0.593 for infinite lattice
size.
Next→
Frank Krauss and Daniel Maitre
Last modified: Tue Oct 3 14:43:58 BST 2017

