It is interesting to study the behaviour near the percolation threshold pc. In fact, this is an example of a second-order phase transition, similar to other better known phase transitions such as the transitions between the paramagnetic and ferromagnetic phases of a metal or melting of materials. Here, the phase transition is between a phase characterised by one large spanning cluster (i.e. macroscopically connected) and a phase dominated by many smaller clusters, i.e. disconnected. Near the transition threshold various properties exhibit a singular behaviour, often described by power laws. One of these properties is the fraction of occupied sites F, which are in the spanning cluster, as a function of p.
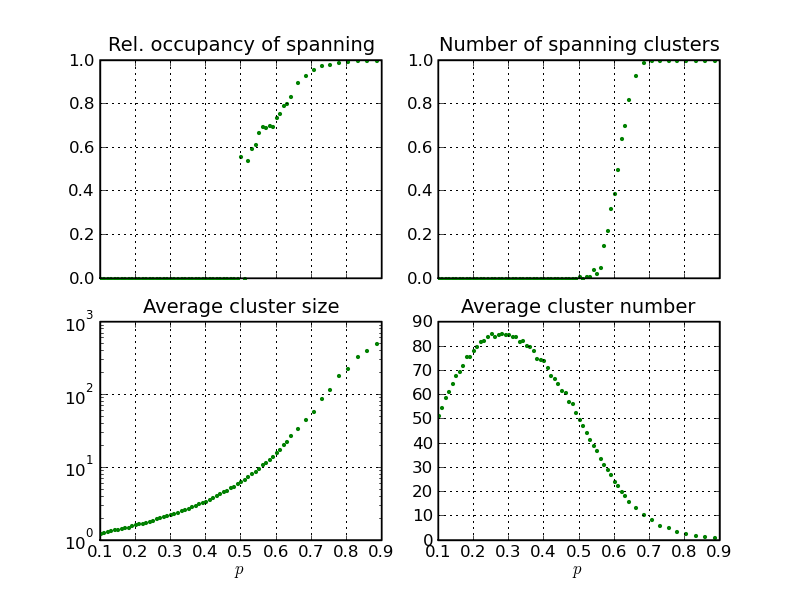
In the plot below, we show the fraction of occupied sites in the spanning cluster, the number of spanning clusters, the average size of all clusters in a filled lattice, and their average number, all as functions of p. We used again a square lattice, here with 25 sites in each direction.

We see that both the number of percolating clusters and their relative occupancy drops precipitously just below 0.6, and it seems to be heading to 0 very quickly (for the relative occupancy this trend is stopped by the finite size of the lattice). This motivates us to suggest that the variation of both quantities around the value where they hit rock bottom is given by power laws of the form
Here β and γ are known as critical exponents. For infinitely large lattices, finite size effects do not matter any more, and p0 tends to the critical concentration pc. Independently of the fact that our plots are not accurate enough to allow for a determination of the critical exponents, it seems obvious that
for p→ p0. In fact, β could analytically be calculated, with the result β = 5/36 for all two-dimensional lattices, independent of their geometry. It is worth stressing that the form of the critical behaviour, represented by a power law, is typical for second-order phase transitions.
Another point is worth noting here: For infinite lattices, the percolating cluster has infinite size, but the fraction of its occupied sites goes to zero, F→ 0. This is very unusual: An object with infinite large extent, but no volume - it must be a fractal!