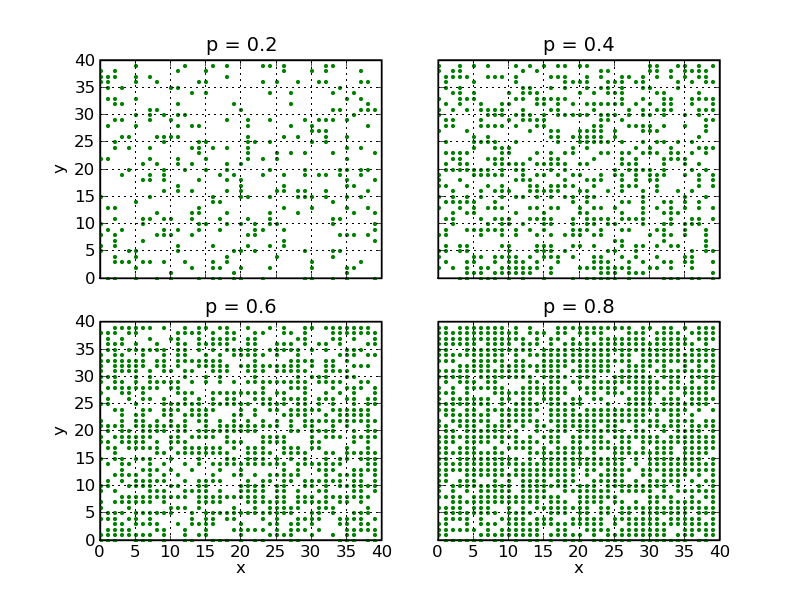
The motion of ground-water through soil, the strength of a porous network, and the flow of oil through a porous rock all fall under a general class of problems known as percolation: Random processes where cells with a finite size within an area or volume are filled or activated. The most basic percolation problem is illustrated in the plot below:

There a square lattice of dimension 40 has been filled randomly, each site with a probability p.
Let us now look a bit closer into the outcomes of the simulation above. To do so, let us first introduce the idea of a "cluster". We define it here such that two occupied sites are said to belong to the same cluster if they have a common edge, i.e. if they are nearest neighbours. This is identical to the definition used before in the cluster growth models. We see that for p=0.2, the pattern has many clusters consisting of one or two sites only - there are barely sites that are not isolated and in principle all clusters are small. Increasing p to 0.4 results in increasing cluster sizes, which now are of the order of around 10 particles. This trend continues with rising p, and at p=0.8, we have more or less one huge cluster including the full lattice with only a small fraction - around 20% - of unoccupied sites. The most interesting structure is to be found at p=0.6. There, it is quite likely that there is one cluster, called the spanning cluster, which touches all four edges of the lattice. This is a typical configuration for this value of p. If such a cluster exists, it is said to percolate. Typically, for this range of p, the spanning cluster would decay into two non-spanning clusters by removing a single site here or there - in other words, the occupancy of single sites may have drastic effects on the characteristic size of clusters. It is interesting to analyse this situation as a function of p. It turns out that the transition from a regime without percolating clusters to a regime with a percolating cluster is quite sharp. It also depends on the size of the lattice d. In the limit of d→∞, the critical value of p roughly is pc=0.593, explaining why our example with p=0.6 is so interesting. At this point it is worth noting that the emergence of a spanning cluster is connected with oil in fact oozing (scientifically speaking: percolating) through the porous rock or with all trees in a wood burning down in a large-scale forest fire.
But how can we calculate/deduce this critical value? This problem is different from the ones encountered so far, since it involves analysing the lattice and checking whether there is a spanning cluster or not, essentially a pattern recognition problem. Such problems are typically quite complicated to solve, if a solution is achievable at all. So, how can we tackle this problem? A simple algorithm would look like this: We chose sites at random and occupy them one after the other. As soon as we have a spanning cluster we stop the procedure, the site occupancy at that moment gives a statistical estimate of pc. Repeating this procedure a number of times will improve the significance of the estimate. The apparent problem here is that the decision of whether the occupancy of an individual site creates a spanning cluster or not is not local for the site, but the necessary information spreads over the full lattice. So we have to find a mechanism to label clusters and their constituting sites to decide whether we have a spanning cluster or not. We can then decide whether or not a cluster in question is percolating.