Percolation

Fractals

Let us now try to quantify this intuitive picture of the difference between Eden and DLA clusters. To do so, we will need a quantitative measure, and this brings us to the concept of fractals. But rather than aiming at a general definition and discussion of this concept, let us try to stick closely to our cluster example.

To introduce the concept of fractals let us consider how we may try to measure the dimensionality of an object (like a line, or a cluster etc.). This may sound like a silly problem, because intuition tells you that lines are of dimension 1, flat disks like our Eden cluster have dimension 2 etc.. But how about a cooked spaghetti, crumpled paper or the like? Well, in principle, they are still one and two-dimensional, respectively (because you would need one or two coordinates to describe points lying on them). On the other hand, it may be worthwhile to come up with an operational definition of dimensionality supplementing this very formal one. We will do this for our example of clusters, but of course, similar reasoning could also be applied to lines and other objects like this.

So, to start with, suppose you have a flat disk in the x-y plane with uniform density σ per area element. Its radius-dependent mass obviously is

\[ m(r)=\sigma\pi r^2\, . \] if we would instead take a straight line with uniform mass density λ per unit length, the length dependent mass would be λl. To be consistent with the example before, we choose a disc of radius r just large enough to include the line (therefore l=2r). Then the r-dependent mass reads \[ m(r)=2\lambda r\, . \] In both cases, the masses scale as r² and r¹, respectively, and the spatial dimensionalities in both cases are 2 and 1. This forms the basis of an operational definition of effective dimensionality, d_f, of a cluster. It reads \[ m(r) \sim r^{d_f}\, , \] where d_f is the fractal dimensionality of the cluster. Applied to the two trivial example cases above, we find \[ \begin{eqnarray*} d_f (\mathrm{disc}) &=& 2 \\ d_f (\mathrm{straight\,\,line}) &=& 1 \, . \end{eqnarray*} \]

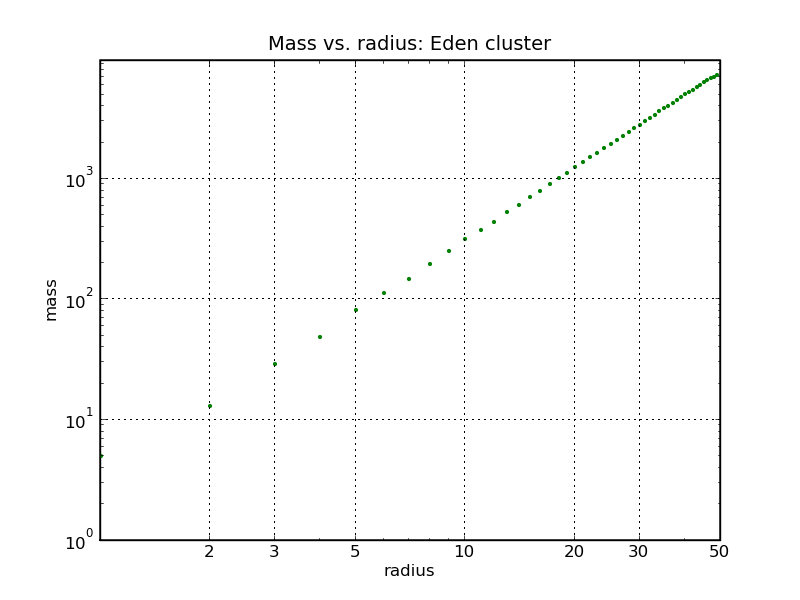
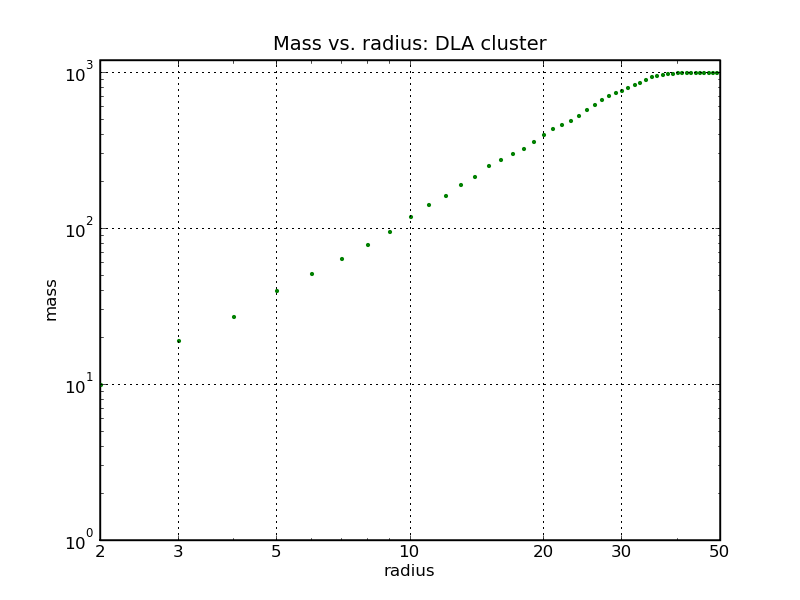
To apply this definition to our clusters, we need to calculate the mass inside a circle with radius r, centred inside the cluster. For convenience we choose the position of the initial seed as the centre. Assuming all particles to have the same mass, we can find m(r) by counting the number of particles inside a radius r around the seed. Obviously, for each cluster generated we can do many of these measurements, varying r from 0 to the size of the cluster, and we can sample over many clusters (10 in the plots below) to accommodate for fluctuations. Looking at the form of the definition, it turns out that a log-log plot is probably a good idea: Taking the log on both sides of the definition above yields

\[ \log m(r) \sim d_f \log r \, . \]

For both clusters, i.e. in both plots, we find a straight line for small enough r. For larger r, this straight line bends over to a horizontal one - this is the effect of having generated clusters with a fixed number of particles only, something like a "finite size effect". For large enough r, the entire cluster will be in the circle, and m(r) becomes independent of the radius. By inspection we find for the two clusters

\[ \begin{eqnarray*} d_f(\mathrm{Eden})&=& 1.99 \\ d_f(\mathrm{DLA}) &=& 1.65 \, . \end{eqnarray*} \]

This substantiates our intuition: The Eden clusters behave like solid discs, having a fractal dimension like such an object, while the DLA clusters are much more fluffy. The catch for the DLA cluster is the following: Naively, we would assume that the open spaces embedded in it would be enough to yield a fractal dimension different from 2, but this is not the case. If the ratio of open to occupied sites is constant, this cancels out and the fractal dimension is still 2. In contrast, in order to have a fractal dimension smaller than 2, the proportion of open sites must increase with r. This evidently is fulfilled by the DLA clusters.

Frank Krauss and Daniel Maitre

Last modified: Tue Oct 3 14:43:58 BST 2017