Percolation

Cluster growth models

In the last lecture we extensively discussed random walks and their connection to diffusion and the approach to equilibrium. We will now turn our attention to another random process with a close relation to random walks, namely the growing of clusters. This is a phenomenon that often appears in nature: Starting from a comparably small seed, larger structures emerge. This can happen a number of ways, to have some idea on the variety consider phenomena like the emergence of a cancer tumor, starting from a single cell, or the growth of snowflakes. In fact, the two models that we will examine now are closely related to these two modes of cluster growth. In presenting them, we will restrict ourselves to two dimensions; an extension to more dimensions, however, should be straightforward. In both cases now we will work on a two-dimensional lattice, where the allowed sites for the particles forming the clusters are given by x or y being an integer. In both cases, we begin by placing a seed particle at the origin of our plane, i.e. at x,y=0. The differences in both growth models are now in how exactly new particles "dock" to that seed.

The subject of this lecture is discussed in chapter 7 sections 6-8 of Giordano & Nakanishi

1. The Eden model:
   In this model, the next particle can be added to any nearest neighbour, (±1,0) or (0,±1), but the exact location is chosen at random. We will call such yet unoccupied sites that are nearest neighbours to an occupied one the perimeter sites. This can obviously also include sites that are completely surrounded by occupied ones. At each step now, a perimeter site is chosen at random and a particle is added, rendering it occupied, and, thus, a cluster site. The process of turning perimeter to cluster sites is repeated and the cluster growth continues until a cluster of the desired size has formed. An example cluster with 1000 particles and its growth is shown below.

   

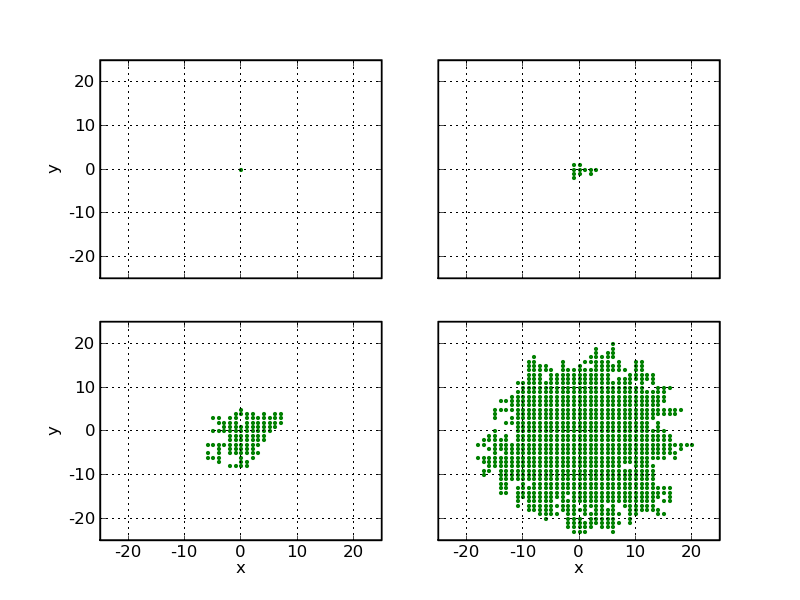
   Clearly it grows a bit like a sphere, with a fuzzy edge and some holes in it. They eventually get closed, since such perimeter sites are not treated differently from the outer ones. This model is sometimes also referred to as the "cancer model", since cancer tumors typically grow like this.

2. Diffusion-limited aggregation (DLA):
   However, not all clusters grow like in the Eden model - as an example take snowflakes, where the cluster forms by particles adding to the cluster that come in from the outside and at some point connect with the cluster. This behaviour is captured by a model called diffusion limited aggregation, or DLA. The rules for the growth of such a cluster are as follows: Particles come in from the outside, from a place chosen at random, sufficiently far away from the cluster. They perform a random walk, and when they hit a perimeter site, they stick to the cluster. This is repeated with as many random walkers as needed until a cluster of the desired size has grown. An example cluster with 512 particles and its growth is shown below.

   

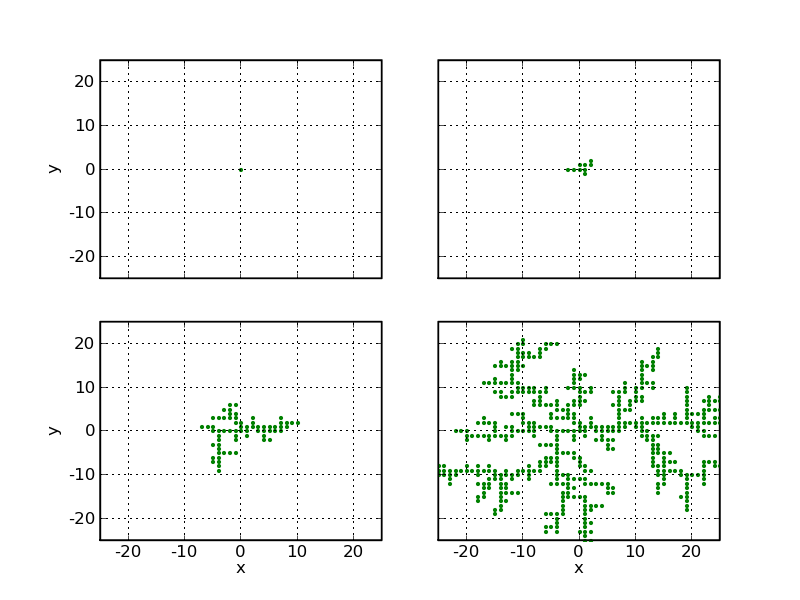
   There's an apparent difference to the Eden-type cluster above - while the Eden cluster is more or less a solid disk, the DLA cluster is a much more fluffy object, with large holes in it and a very irregular shape.

Next→