Harmonic motion

← Previous

Euler method and its breakdown

Let us now consider a numerical approach to this problem, which will serve as a warm-up exercise for the more involved physics problems to be tackled later. In addition, this seemingly harmless warm-up exercise will already present us with an unexpected problem.
As in the case of the cannon-ball trajectory encountered before, we start with the equation of motion,

\[ \frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}\,=\, -\frac{g}{l}\theta\, , \]
and we rewrite this second-order differential equation as two first-order ones:
\[\begin{eqnarray*} \frac{\mathrm{d}\theta}{\mathrm{d}t}\,&=&\,\omega \\ \frac{\mathrm{d}\omega}{\mathrm{d}t}\,&=&\,-\frac{g}{l}\theta \,\, . \end{eqnarray*} \]
In order to prepare this for direct implementation, we again discretise time, leading to
\[\begin{eqnarray*} \theta_{i+1}\,&=&\,\theta_i\,+\,\omega_i\Delta t\\ \omega_{i+1}\,&=&\,\omega_i\,-\,\frac{g}{l}\theta_i\Delta t\,\, , \end{eqnarray*} \]
where
\[\theta_i\,=\,\theta(t_i)\, , \,\,\, \omega_i\,=\,\omega(t_i) \]
and where ti = t0+iΔt, as before.

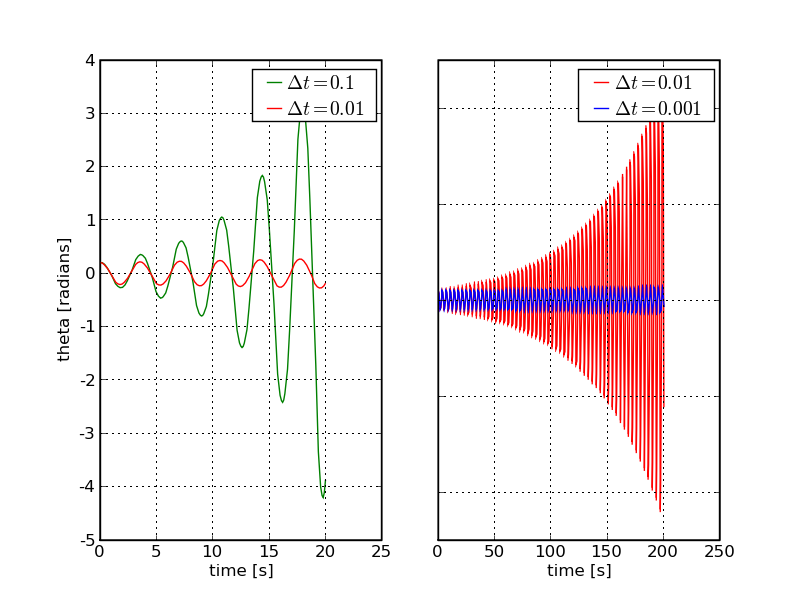
In the plot below, however, we can notice a peculiar behaviour: The amplitude of the oscillation increases over time, and, in accordance with this finding, the energy must also increase. Both are in striking contradiction to the analytical findings above. It is worth stressing at this point that this non-conservation of energy can be reduced by minimising the time step Δ t (in the plots below we used Δ t= 0.1, 0.01, 0.001s for l = 1m and g=9.81m/s², with an initial displacement &theta0=0.2). This energy non-conservation will, however, show up in any case - the pendulum just has to run long enough. So, apparently, for oscillatory motion, the Euler method does not respect the conservation of energy that you would expect from a frictionless motion.

Theta as a function of time for the simple pendulum with the Euler method

We will see that this unphysical behaviour is indeed related to a shortcoming of the Euler method; analysing the origin in more detail will lead to a solution to this problem.

Next →




Frank Krauss and Daniel Maitre
Last modified: Tue Oct 3 14:43:58 BST 2017