Root finding & integration

Numerical integration: Trapezoidal, Simpson and all that

Another problem often encountered in theoretical physics is the occurrence of an integral that is difficult or impossible to evaluate in closed form, i.e. analytically. A typical example for this is the period of the non-linear pendulum, encountered in Lecture 4. Its equation of motion reads

\[ \frac{{\rm d}^2\theta}{{\rm d}t^2} \,=\, - \frac{g}{l}\sin\theta . \]

This can be translated into an equation for the period, namely

\[ T\,=\, \sqrt{\frac{8l}{g}} \, \int\limits_0^{\theta_{\rm max}}\, \frac{{\rm d}\theta}{\sqrt{\cos\theta\,-\,\cos\theta_{\rm max}}}\, , \]

where θ_max is the maximal deflection, in the case studied here equal to the initial deflection. This essentially is an elliptic integral, which cannot be solved analytically, and numerical methods must be applied. We will use it as the example in the following.

Simple Newton-Cotes method

The first class of methods we will employ go under the name of Newton-Cotes methods. They essentially boil down to dividing the region of integration in equally sized intervals: If the integral of a function f(x) is to be taken in the interval [a,b], then we may write

\[I_f^{a,b}\,=\, \int\limits_a^b\,{\rm d} x\,f(x)\approx \sum_{i=0}^{N-1}\,f(x_i)\Delta x\,\,,\] where &Delta x = (b-a)/N and x_i = a+iΔx. To find the error in this approximation we must apply some semi-obscure maths formulae, starting with the Euler-Maclaurin summation formula. It states that \[ \sum_{i=1}^{N-1}\, F(i)\,=\, \int\limits_0^N\,{\rm d}uF(u)-\frac{1}{2}[F(0)+F(N)]+ \sum_{k=1}^{\infty} \left\{ \frac{B_{2k}}{(2k)!} \left[ F^{(2k-1)}(N)- F^{(2k-1)}(0) \right] \right\}\, . \] Here F(x) is a function that can be differentiated any number of times, and F^(k) is the k-th derivative of this function. The constants B_2k are the Bernoulli numbers. Here it should suffice to state that B₂=1/6 and B₄=-1/30 . In order to make the summation formula any use, we need to convert it from the i and u arguments in the function to x space. This can be achieved by the transformation \[ x\,=\,u\Delta x+ a\, . \] With this transformation, the values of u=i can be directly read off: they are just the x_i. Therefore, the Euler-Maclaurin formula (for F=f) becomes \[ \sum_{i=1}^{N-1}f(x_i)\,=\, \frac{1}{\Delta x}\int\limits_a^b{\rm d}xf(x)-\frac{1}{2}[f(a)+f(b)]+ \sum_{k=1}^\infty \left\{ \frac{B_{2k}}{(2k)!} \left[f^{(2k-1)}(b)-f^{(2k-1)}(a) \right]\, (\Delta x)^{2k-1} \right\} \,\, . \] Rearranging and adjusting the summation index on the cost of some extra signs yields the error estimate of the Newton-Cotes method: \[ \int\limits_a^b{\rm d} x\,f(x)\,=\, \sum_{i=0}^{N-1} f(x_i) \Delta x + \frac{\Delta x}{2} [f(b)-f(a)]- \frac{(\Delta x)^2}{12} [f'(b)-f'(a)] + {\cal O}[(\Delta x)^4] \, . \] We see that the Newton-Cotes method has an error of the order Δx, similar to the Euler method for solving differential equations. This, of course, can be addressed by minimizing Δx, but this is not very cost effective.

Trapezoidal method

Fortunately, in this case, the error estimate lends itself to an improvement of the situation. Just adding the second term to the integral estimate, i.e. taking

\[ \int\limits_a^b{\rm d}x\,f(x)\,=\, \sum_{i=0}^{N-1}f(x_i)\Delta x + \frac{\Delta x}{2} [f(b) - f(a)]\,=\, \sum_{i=1}^{N-1}f(x_i)\Delta x + \frac{\Delta x}{2} [f(a) + f(b)] \] immediately reduces the error to the order (Δx)². A closer inspection reveals that the trapezoidal method sums over panels with the forms of trapezes, each with an area of Δx[f(x_i+1)+f(x_i)]/2. In the original Newton-Cotes method rectangular panels were used, with the area given by Δxf(x_i), employing only the left edge of the rectangles. As already indicated, the trapezoidal method has an error of the order of (Δx)², analogous to the second-order Runge-Kutta method for solving differential equations.

Simpson's method

This can be further improved by the methods which use higher-order curves rather than simple zeroth or first order rectangular or trapezoidal panels. A prime example is Simpson's method, which employs parabolae, i.e. curves of second order, that are obtained by fitting parabolic curves through the three top corners of two neighbouring panels. Fitting e.g. the two panels A_i (between x_i and x_i+1) and A_i+1 (between x_i+1 and x_i+2) with the same parabola of the form ax²+bx+c, the area of the two panels reads

\[\begin{eqnarray*} A_i+A_{i+1}\, &=&\, \int\limits_{x_i}^{x_{i+2}}{\rm d}x(ax^2+bx + c)\,= \, \frac{a}{3} (x_{i+2}^3\,-\,x_i^3 )+\frac{b}{2} (x_{i+2}^2-x_i^2 )+ c(x_{i+2}-x_i) \\ &=&\, \frac{a}{3}(x_{i+2}-x_i)(x_{i+2}^2+x_{i+2}x_i+x_i^2) + \frac{b}{2}(x_{i+2}-x_i)(x_{i+2}+x_i) + c(x_{i+2}-x_i) \\ &=&\, \frac{\Delta x}{3} \left[ a(x_{i+2}^2 + 4x_{i+1}^2 + x_i^2) + b(x_{i+2} + 4x_{i+1}\,+\,x_i) + 6c \right] \\ &=&\, \frac{\Delta x}{3} [f(x_{i+2}) + 4f(x_{i+1}) + f(x_i)]\, . \end{eqnarray*} \] Here, the identities \[ x_{i+1} \,=\, \frac{x_{i+2} + x_i}{2} \,\,\, \mathrm{and} \,\,\, \Delta x\,=\, x_{i+2} - x_{i+1}\,=\, x_{i+1}- x_i \] have been used. Therefore, Simpson's rule for the entire integral reads \[ \int\limits_a^b {\rm d}xf(x) \approx \frac{\Delta x}{3}[f(a) + 4f(x_1) + 2f(x_2) + 4f(x_3) + 2f(x_4) + \dots + 2f(x_{N-2})\,+\,4f(x_{N-1}) +f(b)] \] and N is an even number. Here the error is of order (&Delta x)⁴, similar to the fourth-order Runge-Kutta method.

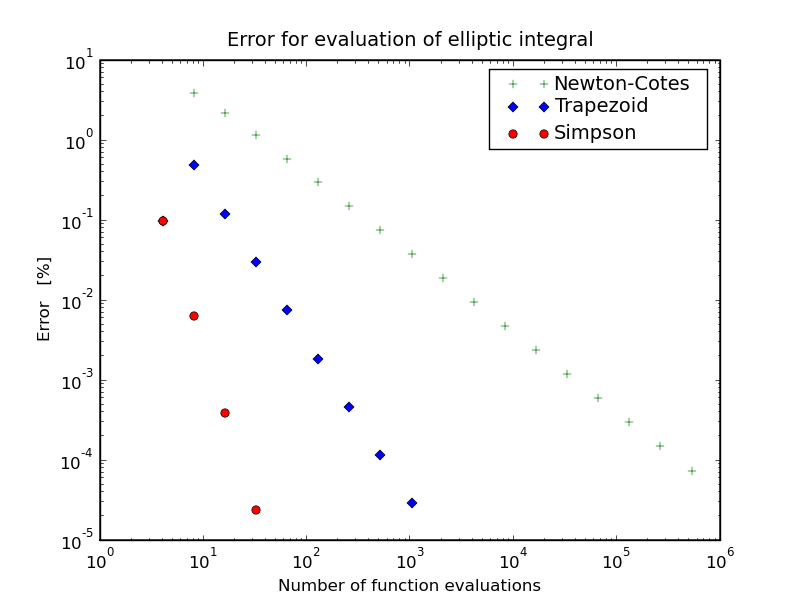
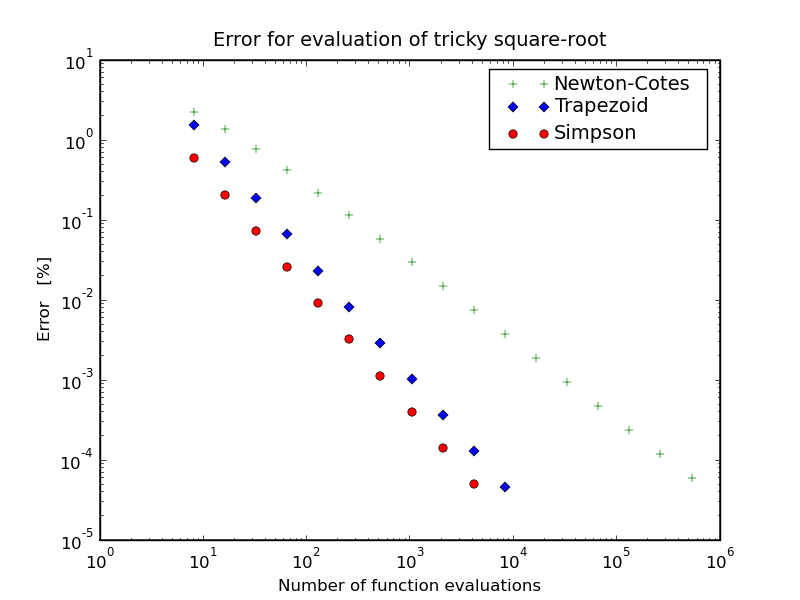
In the table below you'll find some example results for the following two integrals:

\[ \begin{eqnarray*} I_1\,&=&\,\int\limits_0^{\pi/2}{\rm d}\theta\,\sqrt{1 - k^2 \sin^2 \theta} \\ I_2\,&=&\,\int\limits_0^2{\rm d}x\, \sqrt{4-x^2} \, . \end{eqnarray*} \] While the first integral, depicted to the left, converges extremely fast for Simpson's method, the behaviour of the second integral is not as nice. This is mainly due to the fact that the derivative diverges at the right edge.

Frank Krauss and Daniel Maitre

Last modified: Tue Oct 3 14:43:58 BST 2017