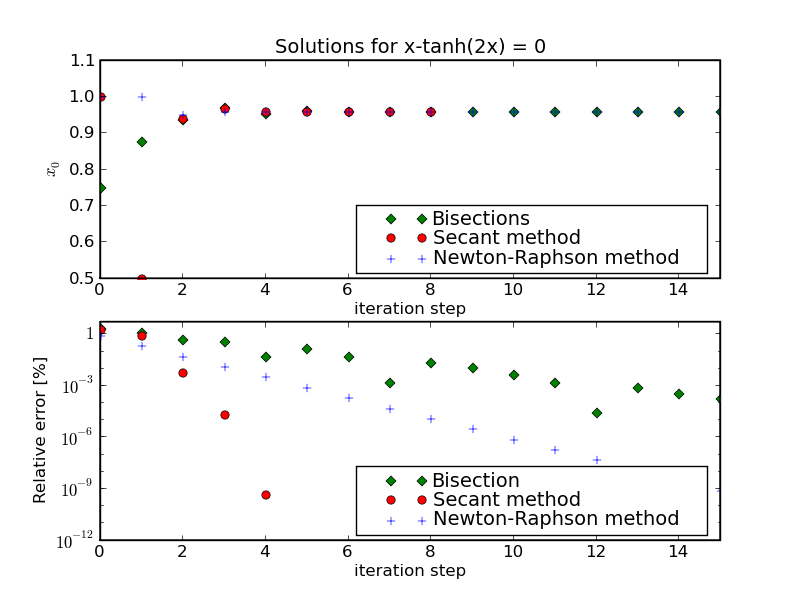
An alternative, and very robust, method to find the roots of an equation is called bisection. It is well known that if a function is continuous in the interval [a,b] and f(a) and f(b) have different sign, then there must be at least one value x for which f(x)=0. The idea of bisections is now to iteratively reduce the size of the interval, until b-a≤ p. This is done by checking the value at the midpoint of a and b, i.e. f(c) for c=(b-a)/2, and then the half-interval is chosen, for which the endpoints a or b and c have opposite signs. Results for the previous problem, this time including the bisection method, are shown below:

Obviously, the convergence behaviour is inferior with respect to the other two methods. It is quite straightforward to convince oneself that its convergence scales only linearly in the steps. However, the big advantage of this method is its robustness.