Root finding & integration

In contrast to the lectures before, this lecture will centre around technical rather than physical problems, namely the solution of equations of the type

\[ f(x)\,=\,0 \]

for x, and the evaluation of integrals,

\[I_f^{a,b}\,=\,\int\limits_a^b \,\mathrm{d}x\,f(x)\,\, , \]

both potentially also in more than one dimension.

This lecture follows the discussion in Giordano & Nakanishi, appendices B, section 1, and E, sections 1, 2, and 4.

Root finding: Newton-Raphson methods

We first address the issue of finding the roots of the equation f(x)=0. We notice that this may help to find extremal values of an equation g(x), if dg(x)/dx = f(x), a typical optimisation problem. Let us first consider a case where we also know the first derivative of f, f'. In this case the method of choice is the Newton-Raphson method. It is an iterative method, based on truncating the Taylor series of f(x) after the first term. Let the unknown true root be X, which is estimated by x_i. Defining Δx_i = x_i-X and Taylor expanding f(X) around x_i, we have

\[ f(X\,=\,x_i-\Delta x_i)\,=\,f(x_i)-f'(x_i)\Delta x_i+ {\cal O}\left[ (\Delta x_i)^2\right]\, \neq\,0 \, , \]

leading to an improved estimate

\[ x_{i+1}\,=\,x_i-\frac{f(x_i)}{f'(x_i)}\, . \]

This is a better estimate of X if Δx_i is small enough. Although this approximation stems from a first-order truncation, the errors Δx_i may decrease very rapidly if the function does not fluctuate to wildly. To see this, rewrite the equation above as

\[ X+\Delta x_{i+1}\,=\,X+\Delta x_i- \frac{f(X+\Delta x_i)}{f'(X+\Delta x_i)}\, . \]

Re-expanding this in a Taylor series then yields the following result:

\[ \begin{eqnarray*} \Delta x_{i+1}\,&=&\, \Delta x_i- \frac{\Delta x_if'(X) + \frac{1}{2}(\Delta x_i)^2f''(X) + {\cal O} [ (\Delta x_i)^3 ] } {f'(X) + \Delta x_i f''(X) + \mathcal{O} [(\Delta x_i)^3] } \\ & & \vphantom{5} \\ &=&\,\frac { \frac{1}{2} (\Delta x_i)^2 f''(X) + {\cal O} [(\Delta x_i)^3] } { f'(X) + \Delta x_i f''(X) + {\cal O}[ (\Delta x_i)^3 ] }\,=\, \left( \frac{ f''(X) }{ 2f'(X) } \right) ( \Delta x_i )^2 + {\cal O} [ (\Delta x_i)^3 ] \, . \end{eqnarray*} \]

In other words: The size of the error decreases quadratically with each iteration step. Therefore, the order of convergence of this method is 2. If f(x) is sufficiently smooth or if the initial estimate, x₀, is close enough to X, the convergence will be fast, but there are cases where this method does not converge at all.

How can this be used in cases where no information concerning the first derivative is available? The answer is to use the function itself to obtain an estimate for the derivative. Recalling that the derivative is defined through the limit

\[ f'(x)\,=\,\lim_{\Delta x \rightarrow 0}\, \frac{f(x + \Delta x) - f(x)}{\Delta x}\, ,\]

it is clear that it can be estimated through

\[ f'(x_i)\, \approx\, \frac{f(x_i) - f(x_{i-1})}{x_i - x_{i-1}}\, . \]

Substituting this estimate into the expression for x_i+1 yields

\[ x_{i+1}\,=\,x_i - f(x_i)\frac{x_i - x_{i-1} }{f(x_i) - f(x_{i-1}) }\, .\]

The error estimate is now given by

\[ \Delta x_{i+1}\,=\,\frac{1}{2}\,\cdot\,\frac{f''(X)}{f'(X)} \Delta x_i\Delta x_{i-1}+ {\cal O}[(\Delta x_i)^3,\, (\Delta x_i)^2\Delta x_{i-1},\, \Delta x_i(\Delta x_{i-1})^2,\,(\Delta x_{i-1})^3]\, . \]

Interestingly, the order of convergence in this case equals the golden mean, (1+√5)/2, roughly 1.6. This method, sometimes also known as the secant method has all the shortcomings of the original Newton-Raphson method, and in addition two initial guesses are necessary.
In order to see the differences of the two methods, let us exemplify them by solving the equation

\[ f(x)\,=\, x - \tanh(ax)\,\equiv\, 0\, , \]

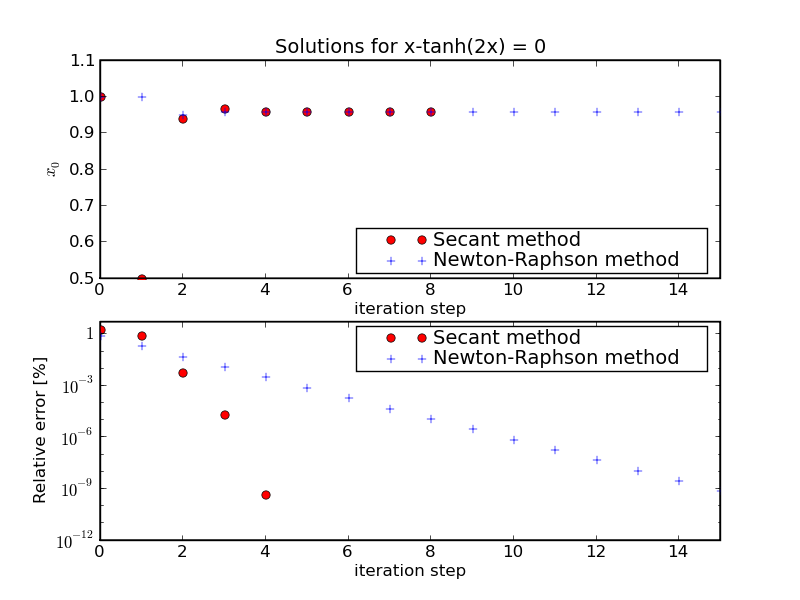
which we will meet again in lecture 8. Here, a is an essentially free parameter: For a≥1, this equation has two non-trivial solutions, at x=±X, while for a≤1 there is only one solution at x=0. Below we see the results for a = 2 obtained from both methods:

Playing with this code it becomes apparent that the level of convergence, and the result depend on the initial values: Choosing, for instance, a different initial value of x₀= 0.5 for the Newton-Raphson method yields the trivial solution x=0.
It is worth noting here that a condition to stop the recursion is given by

\[ \left| \frac{x_i\,-\,x_{i-1}}{x_i\,+\,x_{i-1}} \right| \,\leq\, p\, . \] with p the precision goal, here p=1.e-12. This clearly yields a relative precision and is of little use for the trivial solution. Therefore we supplemented this with the condition that the recursion continues while |x_i-x_i-1|≥ p.

Frank Krauss and Daniel Maitre

Last modified: Tue Oct 3 14:43:58 BST 2017