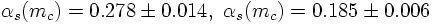It is possible to calculate the decay rate of quarkonia states into hadrons mediated by annihilation into gluons.
However, the decay rates depend on the quarkonia decay constants or, equivalently, on the quark wave function values at the origin.
Although Lattice QCD is nowadays able to calculate decay constants it is possible to determine αs without relying on the knowledge of decay constants at all:
This is achieved by building the ratio between the QCD process under consideration and QED anihilation process. In such a ratio the decay constant or the dependence on the quark wave function value at the origin cancels.
EXAMPLE: ηc DECAYS
The same can be done for the charmonium state ηc with the two quark spins being anti-parallel and the quantum numbers JPC=0-+. Its mass (2.980 GeV) is slightly smaller than the J/Ψ mass (3.097 GeV).
The ηc meson can not be produced in electron-positron annihilation via one virtual photon due its C quantum number. However, it can be produced by a primary production of a J/Ψ which decays into ηc + γ due to a magnetic dipole transition resulting a quark spin-flip.
With these quantum numbers assigned the ηc decays into hadrons mediated by a two-gluon annihilation. The decay width in the non-relativistic limit is given by
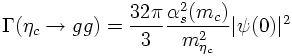
Parallel in line, the ηc decays into two photons is
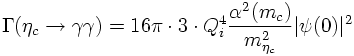
In full analogy, one can use bottonium decays to determine αs at the b mass scale and one finds: