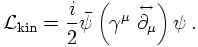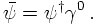The Dirac equation

The real thing

1. Charged spin-½ particles: Two spinors
   
2. Linearisation
   Historically, the main reason for Dirac to construct his equation was not the aim to include particles with spin, but rather to present a solution for the problem concerning the solutions with negative energies. He identified the quadratic form of the Klein-Gordon equation as the source of the problem and, instead, pursued a linear form of the equations of motion and, thus of the Lagrangian. This linearisation is the subject of this section.
   
   

   PRACTISING: TWO-COMPONENT SPINORS

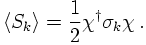
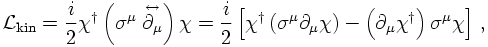
   In a previous section, the spin expectation values have been constructed from the spin states, reading Introducing a helping matrix it is possible to construct a four-vector of Pauli matrices, ready to be contracted with four-vectors such as momenta or derivatives. Then it is possible to construct some simple kinetic term for these two-component spinors, namely where the minus sign reflects the fact that spin-½ particles are fermions. When using a plus sign instead, the result is nothing but a total derivative and thus vanishes. It is also easy to check, that by construction this Lagrangian is real. In fact, it is also the simplest possible kinetic term for spinors, using it implies that the canonical mass dimension of spinors is 3/2.
   
   

   THE REAL THING: BI-SPINORS

   Similar reasoning can be applied to construct a linear mass term for the Dirac (bi-) spinors. There, however, instead of the Pauli matrices, suitable for two-component spinors, new matrices suitable for four-component Dirac spinors need to be introduced. These are the Dirac- or γ matrices. Without specifying them here, a kinetic term for Dirac spinors ψ thus reads As will be seen in more detail later, the "barred" spinor is connected to the "daggered" one through The reason behind this change from daggered to barred spinors is the ordering of the spinors, the γ matrix and the partial derivative.
   
   
3. Equation of motion for particle and antiparticle
   
4. Relativistic invariance: The Dirac algebra
   
5. Spin, helicity and chirality
   
6. The parity of the Dirac spinors
   
7.