Harmonic motion

←Previous

Spicing up the pendulum: Adding dissipation

Let us now make the simple pendulum a bit more realistic by adding dissipation, i.e. a damping force. The assumption typically made in this case is that the friction is proportional to the velocity, such that the equation of motion reads

\[ \frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}\,=\, -q\frac{\mathrm{d}\theta}{\mathrm{d}t} - \frac{g}{l}\theta \, . \]

Since this is still a linear equation, it can easily be solved analytically. The details for the solution can be found in many textbooks on physics; here, it should suffice to state that there are three regimes for the solution, namely

  1. The underdamped regime In this regime the friction is small enough to allow an oscillatory behaviour of the solution, where the amplitude decays exponentially:

    \[ \theta(t)\,=\,\theta_0\exp\left(-\frac{qt}{2}\right)\, \sin\left(\sqrt{\Omega^2\,-\,\frac{q^2}{4}}\,\,t+\phi\right) \,, \]

    where, as before, Ω²=g/l.

  2. The overdamped regime The other extreme is the overdamped regime, where the strength of the friction is so large that the time evolution of the angle is entirely given by an exponential decay,

    \[\theta(t)\,=\, \theta_0\exp\left[ -\left(\frac{q}{2}+\sqrt{\frac{q^2}{4}- \Omega^2} \right)t\right] \, . \]

  3. The critically damped regime At the boundary between these two regimes, the system is said to be critically damped, and the time evolution is given by

    \[ \theta(t)\,=\, (\theta_0+Ct)\exp\left(-\frac{qt}{2}\right) \, \, . \]

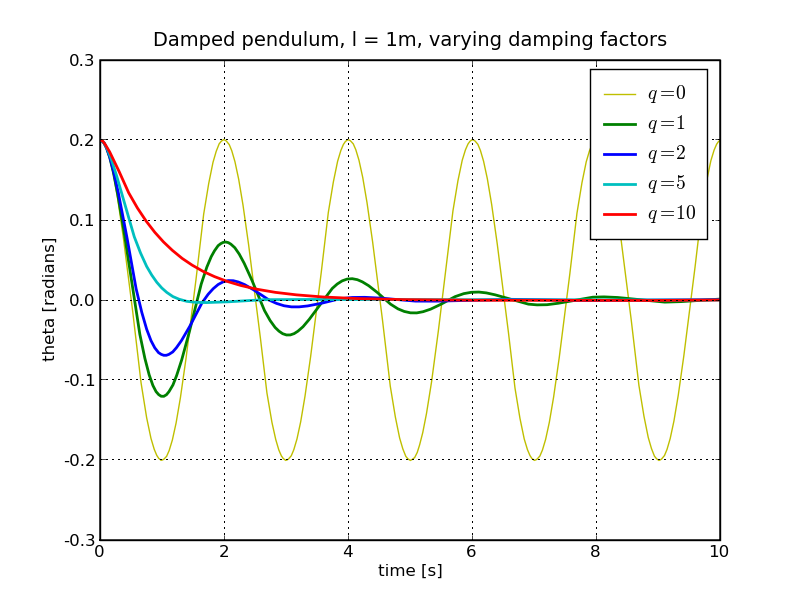
Some numerical results for g = 9.8 m/s², l = 1 m and varying values of q are shown below (for q=5/s the system is close to being critically damped).

Theta as a function of time for the damped pendulum

Obviously, damping results in the pendulum losing energy, typically as heat.

Spicing up the pendulum: Adding a driving force

This is not yet very exciting, so let us add some action. This is best achieved by adding a driving force, which we choose to be of sinusoidal form with fixed amplitude FD and frequency ΩD. Then, the equation of motion is given by

\[ \frac{\mathrm{d}^2\theta}{\mathrm{d}t^2} \,=\, -q\frac{\mathrm{d}\theta}{\mathrm{d}t} - \frac{g}{l}\theta + F_D\sin(\Omega_Dt) \,\, .\]

This driving force will pump energy into the system and the driving frequency will compete with the natural or eigen-frequency of the pendulum. It turns out that this equation, too, can be solved analytically, and the steady state solution after "swinging in" reads

\[ \theta(t) \,=\, \theta_0 \sin(\Omega_Dt + \phi)\,\, ,\]

where the maximal amplitude is

\[ \theta_0 \,=\, \frac{F_D}{\sqrt{(\Omega^2-\Omega_D^2)^2 + (q\Omega_D)^2}} \,\, . \]

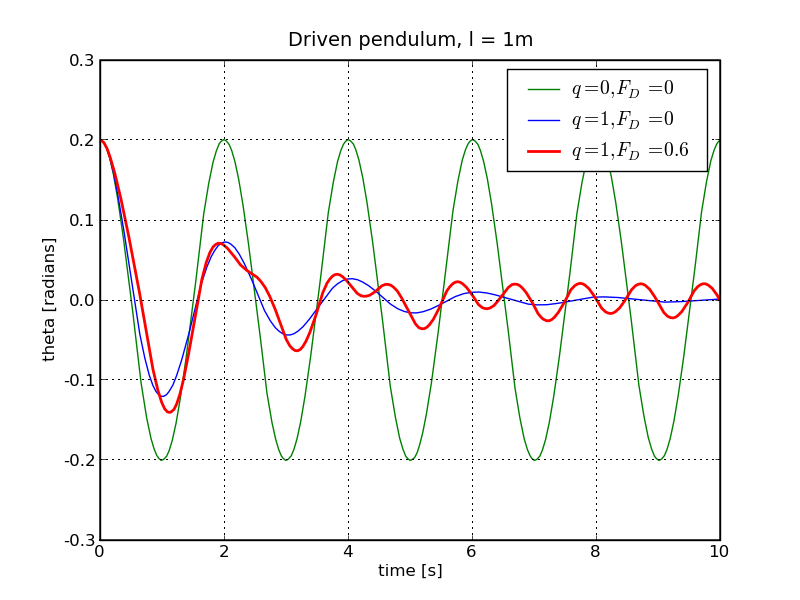
At first sight the driven, damped pendulum shows a somewhat boring behaviour: it just swings with the frequency dictated upon it by the external force. See below for a case where ΩD=2Ω:

Driven pendulum

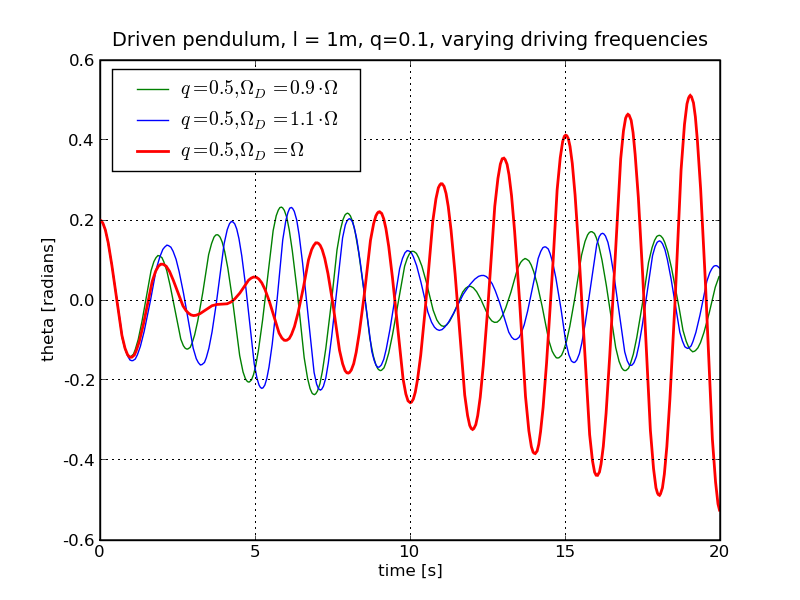
There is an interesting phenomenon, though, namely resonance: the maximal amplitude can become very large in cases where the driving frequency of the external force is identical or nearly identical to the eigen-frequency of the pendulum. This is especially pronounced if the dissipation coefficient, represented by q, is small. Below is the case for FD=0.3 and q=0.1:

Driven pendulum: resonance behaviour

Adding nonlinearity

The last step towards having a more realistic pendulum is to leave the approximation of small deflection angles. This amounts to not truncating the series

\[ \sin\theta\,=\, \theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+\,\dots \]

after the first term - which led to our beautifully linear equation of motion for the mathematical pendulum. Doing that will ultimately lead to a realistic description of a pendulum and to the emergence of deterministic chaos.
This subject, however, will be discussed in the next lecture.

Next→




Frank Krauss and Daniel Maitre
Last modified: Tue Oct 3 14:43:58 BST 2017