Root finding & Integration
←Previous
Hyperspheres
We can extend the previous example, the determination of π from the area of
the unit circle, to the calculation of unit hyperspheres of dimension d. In
Cartesian coordinates we can write for the volume of a sphere with radius r
\[ V_d(r)\,=\,\prod_{i=1}^d \left[ \int\limits_{-1}^1 {\rm d}x_i \right]\,
\Theta\, \left( r- \sqrt{\sum_{i=1}^d x_i^2} \right) \,\, . \]
For hyperspheres with unit radius, a simple replacement r→ 1 is
sufficient. Simple checks show that the equation above yields the volume of
a circle and a sphere for d=2 and d=3, respectively. Obviously,
plugging this into, say, the Trapezoid or Simpson algorithm is quite a painful
exercise. We could, of course, try to alleviate this by rewriting the equation
above in a suitable fashion. A first idea would be to get rid of the
Θ-function with its complicated argument. This boils down to
rewriting the equation above as
\[ V_d(r)\,=\,\prod_{i=1}^d \left[ \begin{array}{c}
\sqrt{r^2- \sum\limits_{j=1}^i x_j^2} \\
\int {\rm d}x_i \\
-\,\sqrt{r^2- \sum\limits_{j=1}^i x_j^2} \end{array} \right]\, ,
\]
but this merely replaces comparatively simple integration boundaries and the
Θ-function, which is simple to deal with in a numerical approach, with
complicated integration boundaries and no Θ-function. So, maybe this
is not a very good idea for a multi-dimensional integral.
Doing it the hard way with, say, the Trapezoid rule, now means that we have to
integrate over a d-dimensional grid, with N bins in each direction.
We leave this as a homework exercise, and move on to the discussion of the Monte
Carlo method. Clearly, implementing the integral over a d-dimensional
hypersphere is a piece of cake, once we have mastered the circle: We just need to
generate d random numbers rather than two and plugging them into a
d-dimensional vector. Again, we calculate the length of the vector and
compare it with the radius (it's better to compare the squares - this avoids
needlessly calculating a square-root). Depending on the outcome, we either book a
"hit", i.e. a 1, or a "miss", i.e. a 0. Doing this for the integration, we're
guaranteed to have the error decreasing like 1/√N with the number of
N trials.
But can we do better? The answer is yes! We can. We just have to transform
our d-dimensional Cartesian coordinates into d-dimensional polar
ones. That sounds harder than it is. To see how this works, let us just take a
look into the equations, expressing the Cartesian coordinates through the polar
ones. We will immediately see (and hopefully be convinced of the correctness of)
the pattern - calculating the Jacobean etc. is quite cheap.
\[ \begin{eqnarray*}
x_1\,&=&\,r\sin\theta_1\,\sin\theta_2\,\dots\,\sin\theta_{d-3}\,
\sin\theta_{d-2}\,\cos\theta_{d-1} \\
x_2\,&=&\,r\sin\theta_1\,\sin\theta_2\,\dots\,
\sin\theta_{d-3}\,\sin\theta_{d-2}\,\sin\theta_{d-1} \\
x_3\,&=&\,r\sin\theta_1\,\sin\theta_2\,\dots\,\sin\theta_{d-3}\,
\cos\theta_{d-2} \\
x_4\,&=&\,r\sin\theta_1\,\sin\theta_2\,\dots\,\cos\theta_{d-3} \\
\vdots\,&\vdots&\,\vdots \\
x_{d-1}\,&=&\,r\sin\theta_1\,\cos\theta_2 \\
x_d\,&=&\, r\,\cos\theta_1\, . \end{eqnarray*} \]
We see that the d Cartesian coordinates have been replaced with one radius
coordinate and d-1 angles. d-2 of them range from 0 to
π, and only the last one covers the range from 0 to
2π. Expressed in these coordinates the d-dimensional volume
element reads
\[ {\rm d}V_d\,=\,\int\limits_0^R r^{d-1}{\rm d}r\,
\left[ \prod_{i=1}^{d-2} \left( \int\limits_0^\pi
\sin^{d-1-i}\theta_i\,{\rm d}\theta_i \right) \right]
\,\int\limits_{-\pi}^\pi{\rm d}\theta_{d-1}\, . \]
Here R denotes the radius of the hypersphere (in our case we will set it
to R=1). Employing the relation
\[\int\limits_0^\pi\sin^{2\alpha +1}\theta\,\cos^{2\beta +1}\theta\,{\rm d}\theta
\,=\,\frac{\Gamma(\alpha+1)\Gamma(\beta+1)}{2\Gamma(\alpha+\beta+2)}
\]
with β=-½ yields
\[ \int\limits_0^\pi \sin^{2\alpha +1}\theta\,{\rm d}\theta\,=\,
\frac{\Gamma(\alpha+1)\Gamma(0)}{2\Gamma(\alpha+3/2)} \]
and therefore
\[ \int\limits_0^\pi \sin^{d-1-i}\theta\,{\rm d}\theta\,=\,
\frac{\Gamma \left( \frac{d-i}{2} \right) }{2\Gamma \left( \frac{d-i+1}{2}
\right)} \]
for each of the angular integrals.
The Euler-
Γ function has many interesting properties. We will list a few
here:
You may think of it as a continuous interpolation of the factorial,
shifted by one. Therefore, for integer, positive arguments,
\[ \Gamma(x+1)\,=\,x\Gamma(x)\,\, ^{\underrightarrow{x \in N}} \,\,x!\, .\]
The recursion starts with
\[\Gamma(0)\,=\,1\, .\]
This also implies that for integer negative values the Γ function
exhibits poles.
Some further specific values include
\[ \begin{eqnarray*}
\Gamma(0)\,&=&\,\Gamma(1)\,=\,1 \\
\Gamma \left( \frac{1}{2} \right)\,&=&\,\sqrt{\pi} \\
\Gamma \left( 1\,+\,\frac{n}{2} \right)\,&=&\,\sqrt{\frac{\pi}{2^{n+1}}}
\,\cdot\,n!!
\,,\end{eqnarray*} \]
where the double
factorial is given by
\[ n!!\,=\,\prod_{i=1,2}^ni\,=\, \left\{ \begin{array}{cc}
1\,\cdot\,3\,\cdot\,5\,\cdot\,\dots\,\cdot\,(n-2)\,\cdot\,n &
n\mathrm{\,\,is\,\,odd} \\
2\,\cdot\,4\,\cdot\,6\,\cdot\,\dots\,\cdot\,(n-2)\,\cdot\,n &
n\mathrm{\,\,is\,\,even\, .} \end{array} \right. \]
There is a number of representations of the Γ-function
through integrals, shown below. For the homework assignment you should take
the one with limits 0 and 1.
\[ \begin{eqnarray*}
\Gamma(z)\,&=&\,\int\limits_0^\infty {\rm d}t\,t^{z-1} e^{-t} \\
&=&\,\int\limits_0^1 {\rm d}u
\left( \ln \frac{1}{u} \right)^{z-1}\, ,
\end{eqnarray*} \]
where the first line in fact is Gauss' definition, commonly used.
The first derivative of the Γ-function reads
\[ \Gamma '(z)\,=\, \frac{{\rm d}\Gamma(z)}{{\rm d}z}\,=\,\Gamma(z)\,
\left( \int\limits_0^1{\rm d}t \frac{1-t^{z\,-\,1}}{1\,-\,t}\,-\,\gamma_E
\right)
\,=\,\Gamma(z)\psi^{(0)}(z)\, , \]
where the Euler-Mascheroni constant is given by
&gammaE = 0.577215665
and where ψ(0) belongs to a group of functions known as
Polygamma-
functions.
Putting this together yields, for the volume of the d-dimensional
hypersphere,
\[ V_d\,=\,\frac{\pi^{d/2}R^d}{\Gamma \left( \frac{d}{2}\,+\,1 \right)}\, . \]
The results are shown below
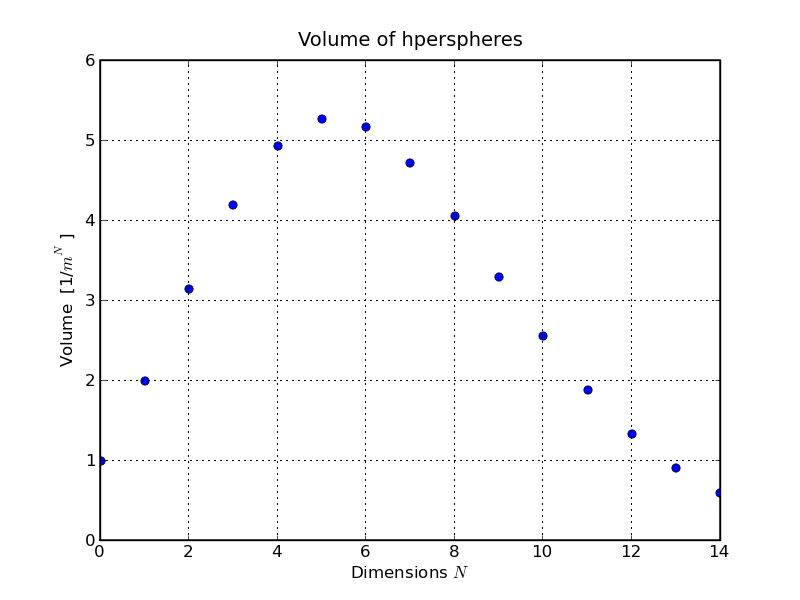
One could guess from the plot that for d→∞, this volume
approaches zero, which is indeed the case. This is because the Γ-
function, being a factorial, grows faster than any power of d. In the
homework exercise we will do something quite fun: We will assume that the number
of dimensions is a real number, not constrained to integers, and we will try to
find the number of dimensions, for which the volume of the unit hypersphere equals
the volume of the unit hypercube, Rn. We will also find the
number of dimensions for which the volume of the unit hypersphere is largest.
It is amusing to note that there are also interesting relations between the
volume and the surface of hyperspheres. From
\[ {\rm d}S_{d-1}\,=\,R^{d-1} \left[ \prod_{i=1}^{d-2} \left(
\int\limits_0^\pi \sin^{d-1-i}\theta_i{\rm d} \theta_i
\right)\right]
\int\limits_{-\pi}^\pi{\rm d}\theta_{d-1}\,=\,
\left. \frac{{\rm d}V_d}{{\rm d}r} \right|_{r=R} \]
we find
\[ S_{d-1}(R)\,=\, \frac{{\rm d}V_d(R)}{{\rm d}R}\,=\,
\frac{{\rm d}V_d}{R}\,=\,\frac{2\pi^{d/2}R^{d-1}}{\Gamma \left( \frac{d}{2}
\right)}\,.
\]
Ultimately we find the following relations between the surface and volume of
d-dimensional hyperspheres:
\[ \frac{V_d}{S_{d-1}}\,=\,\frac{R}{d}\,\,\,\,\mathrm{and}\,\,\,\,
\frac{S_{d+1}}{V_d}\,=\,2\pi R\, , \]
leading to the recurrence relation
\[ V_d\,=\,\frac{2 \pi R^2}{d} V_{d-2}\, . \]
Next→
Frank Krauss and Daniel Maitre
Last modified: Tue Oct 3 14:43:58 BST 2017

