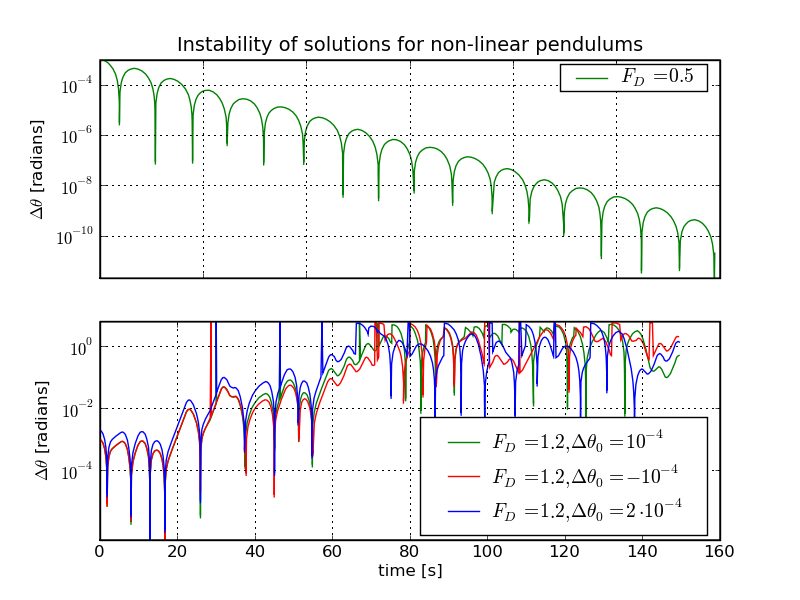
Let us now discuss the stability of the solutions to the differential equations describing the motion of our pendulum. Imagine that we have two identical pendulums, with exactly the same length, l, the same damping factors, q, and the same driving force with identical amplitude, FD, and frequency, ΩD. The only difference stems from a slight inaccuracy in preparing the pendulum, i.e. from the exact value of θ0. We then let both pendulums run and, as before, keep track of the two θ(t), which we call θ1,2(t). Plotting their difference Δθ = |θ1-θ2| for different driving forces is quite revealing. In the plot below we started with &theta0=0.2 and deviations of the order of Δ&theta0=0.001, again for our pendulum with l=9.81m, q=0.51/s and &OmegaD=0.661/s.

While at small driving force the discrepancies vanish with time, they increase for larger driving forces until they reach a plateau. The behaviour for the small driving force is quite simple to understand: In the beginning, the small deviation in the initial angle leads to slightly different periods. This, however, becomes less important, since the original periodic motion decays due to the damping force, and the driving force takes over. It is, however, not strong enough to overcome the dissipative energy loss at all, with the effect that the pendulum remains in a region, where the deflection angles are small and the non-linearity in the equations of motion is not very important. Since, in addition, both pendulums are dominated more and more by the driving force, which is the same for both, we understand that the differences are merely due to the exponentially decaying original eigen-mode of the oscillation. In total this means that the motion is predictable in a stable manner, such that slight deviations in the initial conditions do not lead to diverging patterns of motion.
This is in striking contrast to the case of the strong driving force, where the patterns of motion actually diverge until they reach a plateau - after all the difference of the two angles cannot exceed 2π. This behaviour is caused by the driving force being strong enough to make the pendulum leave the region of small deflections, such that the non-linearity indeed becomes an important feature. Then, slight deviations in the alignment of the pendulum with the driving force lead to large differences. It is interesting to see how rapidly this divergence becomes large. This behaviour again cannot be described by a simple function for Δθ. However, if we sample over many slight deviations, a band emerges, and we can read off that
It turns out that such a behaviour is typical for a certain kind of chaotic systems, which can in turn be characterised by their Lyapunov exponent, λ. For the case of our pendulum at high driving forces this implies that even if we manage to repeat the same experiment quite precisely, we still cannot precisely predict the motion of the pendulum - we can however, estimate the evoultion of differences due to the inaccuracy in its preparation. This is just because already the slightest deviation will "explode" to large differences, given by the exponential form and governed by the respective Lyapunov exponent. In other words: For all practical purposes, at high drives, the pendulum is unpredictable, although it is completely determined by its initial conditions. This extreme sensitivity on initial conditions is the hallmark of deterministic chaos.
One point is worth noting here: The chaotic behaviour of the pendulum can be characterised in both the chaotic and the non-chaotic regime through an exponential form. The sign of their Lyapunov exponents then determines whether the system is chaotic (λ>0) or not (λ<0), with the obvious transition at λ=0.