In this lecture we will discuss chaotic effects in the pendulum.
The subject of this lecture is also discussed in chapter 3, sections 3 and 4 of Giordano & Nakanishi.
As a first example of non-linear effects, let us consider the non-linear pendulum with no friction and no driving force. It is described by
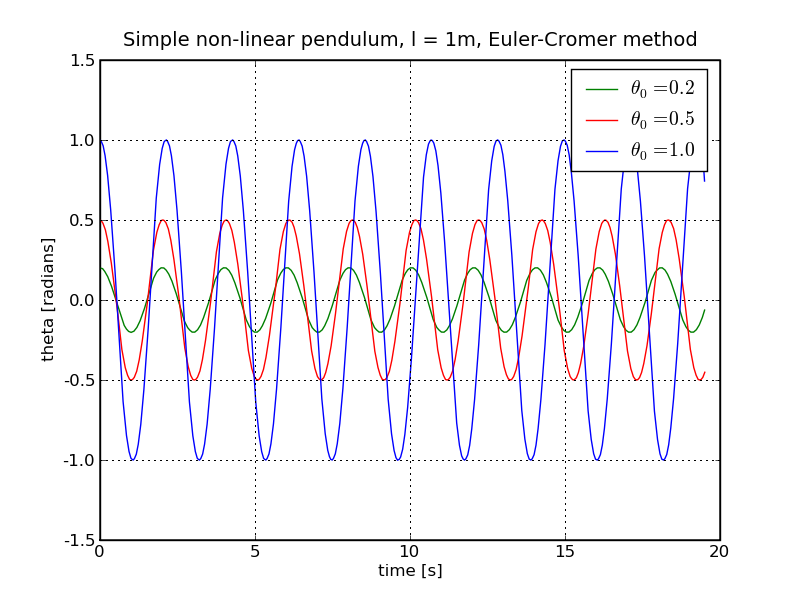
Due to the absence of the driving force and the friction term there is no means to change the energy of the system, which thus remains constant. As a consequence, the system performs a periodic motion. Its period, however, is not a constant anymore, as in the linear case, but it depends on the amplitude, i.e. the initial displacement and velocity. In principle, this could be shown analytically, but we refrain from this quite complicated piece of maths and rather demonstrate this with our numerical tool. The ourcomes of this numerical analysis are displayed below:

A careful analysis would reveal that, although the motion is periodic, it is impossible to describe it with one simple sine or cosine function with a fixed frequency alone. At least, the frequency now depends on the energy of the system, here given by the initial displacement, i.e. the amplitude. In fact, the pendulum spends a increasing amounts of time at the turning points for increasing amplitudes.
However, up to now, nothing really dramatic has happened. We will have more fun, when we start adding dissipation and a driving force. In so doing, care has to be taken with the treatment of &theta: Naively it can take any value, but in practise it pays of to constrain it to the interval [-π, &pi] by adding or subtracting integer multiples of 2π if necessary. Results for both the angles and the velocities are shown below, where only the amplitude of the driving force has been varied, keeping all other parameters fixed (q=0.5 1/s, ΩD = 0.66 1/s, and l=9.81m).
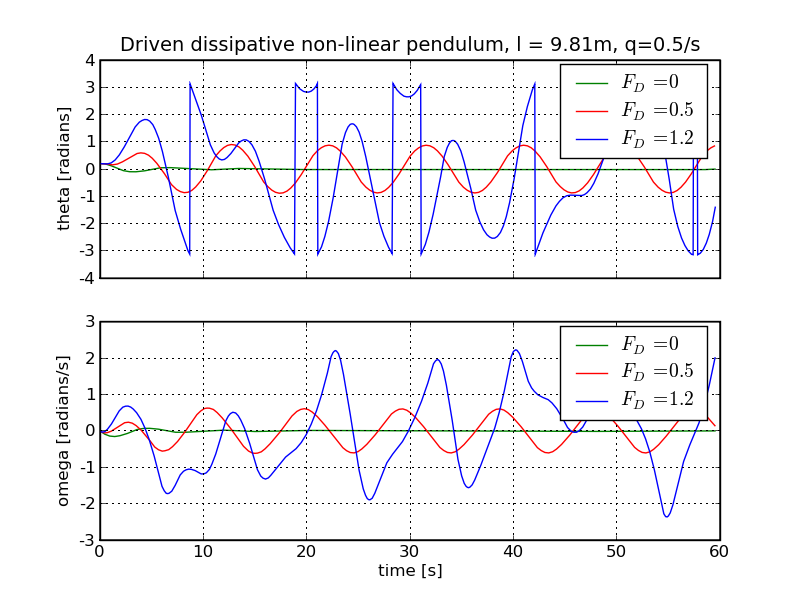
In this plot, the spikes come from the jumps, when the angles are forced to stay in the interval [-π, &pi]. Obviously, with the driving force being absent, there is just a damped motion, which quickly fades out on the scales that we consider in our plot. For the middle value of the driving force's amplitude, FD=0.5, there are two regimes: first of all the original frequency is present, but it quickly decays (gets "damped away") such that only the driving frequency remains. For the large-amplitude driving force, FD=1.2 the motion does not look periodic any more; jumps occur and the pattern of the motion changes progressively and, seemingly, erratically. This, in fact, would hold true independent of how long we let the pendulum run - at sufficiently high values of the driving force, the behaviour of motion never exactly repeats itself, it is chaotic.
This is a finding to be appreciated: At zero driving force, there is just a damped periodic motion, nothing exciting. At low driving force, the motion still is periodic: a simple oscillation, which is determined by the frequency of the driving force once the original frequency modes have decayed. Again, the non-linearity does not massively show up. At sufficiently high drive, however, the motion turns chaotic, and it becomes a very complicated, non-repeating function of time. But what does chaotic now mean? Intuitively we would be tempted to say: unpredictable, but this obviously is not true, although the appearance supports intuition. In fact, we could calculate and thus predict the motion, since it is the differential equation that we could solve. And, from the theory of differential equations, we know that the solution to this type of equation is entirely defined by the initial conditions, e.g. at t=0. So we are left with the seemingly unresolvable contradiction of having chaotic behaviour in a seemingly unpredictable pattern of motion, that is completely determined (and hence deterministic) through our numerical code. So, it is unpredictable and deterministic at the same time. This indeed is what goes under the name of deterministic chaos: Complicated, non-linear differential equations describing a seemingly unpredictable pattern of motion, which in turn has a strong dependence on initial values. We will analyse this behaviour in more detail now.