Electron-Positron annihilation into fermion-antifermion pairs is very important as this is the dominant process at an electron-positron collider.
In QED the first order diagram is a s-channel photon exchange, that is, an annihilation of the electron and positron in a virtual photon decaying in a charged fermion-antifermion pair. These can be either charged leptons (electrons, muons, tau's) or a quark-antiquark pair.
The case of an electron-positron in the final state (Bhabha scattering) is not considered since this reaction is also possible by a photon exchange in the t-channel. In this case, both amplitudes have to be added.
SPIN AVERAGED AMPLITUDE SQUARED
The spin averaged amplitude squared for electron-positron annihilation in a muon-antimuon pair in the high energy limit in terms of the Mandelstam variables is given by
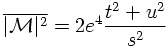
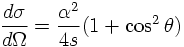
Integrating over θ results in the integrated cross section
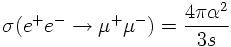
REMARKS
1) The integrated cross section for annihilation shows the typical 1/s QED-behaviour with increasing s.
2) The differential cross section for annihilation in QED is forward-backward symmetric. However, annihilation is also possible in weak interactions by exchanging a (virtual) Z0. Adding the weak and the QED amplitudes leads to a forward-backward asymmetry in the differential cross section.
Measuring this asymmetry was used e.g. at PETRA (DORIS, Desy) in order to extract the Weinberg angle describing the electroweak symmetry breaking.
3) Measuring the differential cross section for electron-positron annihilation in quark-antiquark pairs was used to show that quarks carry spin 1/2.
Quarks do not exist as free particles but do "hadronize" when produced in a high-energy interaction. Therefore, one measures the differential cross section for electron-positron annihilation into hadrons.
If the energies of the quark and antiquark in the final state is large the hadrons formed will carry momenta pointing preferentially in the same direction as the primary quark or antiquark. Typical transverse momenta of the hadrons in the hadronization are of the order 300 MeV.
To "find" the emission direction of the primary quarks from the emerging hadrons, hadron jets are searched for by defining a "thrust" axis.
The angle of the thrust axis with respect to the beam axis for two back-to-back hadron jets shows the same QED-dependence as the annihilation into a muon-antimuon pair! This strongly supports the idea that primary spin-1/2 quark-antiquark pairs are produced in electron-positron annihilations subsequently hadronizing into hadrons which are then measured in the detector.
4) While the integrated cross section for hadron final states in electron-positron annihilation shows in general the typical 1/s behaviour with increasing s there are some prominent peaks at located CMS energies.
At these energies hadron resonances are produced which carry the same quantum numbers as the photon: JPC=1--. That is, these resonances are directly produced by a virtual s-channel photon and decay subsequently into hadrons. These hadron resonances contain quark-antiquark pairs. The prominent ones are: ρ0, ω, φ, J/Ψ, Υ. The dependence of the annihilation cross section as a function of the CMS energy can be found here.
The additional peak around 90 GeV is caused by the production of a real Z0 boson.
5) An important observable as a function of the CMS energy is the ratio of cross sections R:


The measured ratio R (also found here) strongly supports that quarks carry charges Q=2/3 (u, c) and Q=1/3 (d, s, b) and in addition carry 'Color'.