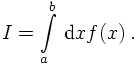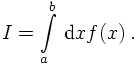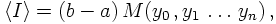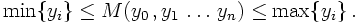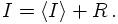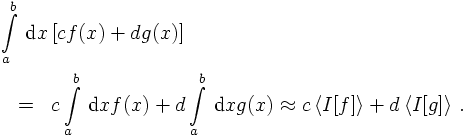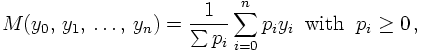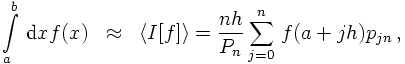Basics
Phase spacing
Simple quadratures
Quadrature in general denotes the (approximate) numerical evaluation of finite
integrals of a function, commonly in one dimension, from the knowledge of some
specific values of the function in question, i.e. the numerical calculation of
I given by
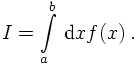 Here, the function f is assumed to be sufficiently continous. The integral
I can be approximated by
Here, the function f is assumed to be sufficiently continous. The integral
I can be approximated by
 This can be readily improved, by adding more and more sampling points
yi=f(xi), such that the integral can be estimated as
This can be readily improved, by adding more and more sampling points
yi=f(xi), such that the integral can be estimated as
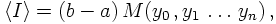 where M denotes some suitably defined average value of the sampling points. Of course,
where M denotes some suitably defined average value of the sampling points. Of course,
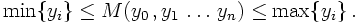 Note that here the exact value of the integral I has already been replaced by an
estimator <I>, the difference between both is some residual term R, which has been
omitted here. In fact, in this notation,
Note that here the exact value of the integral I has already been replaced by an
estimator <I>, the difference between both is some residual term R, which has been
omitted here. In fact, in this notation,
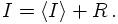 In order to alleviate the usage of this approach M should fulfil some conditions:
In order to alleviate the usage of this approach M should fulfil some conditions:
- M should be linear, i.e.
 This guarantees that linear combinations of integrals can be estimated by
linear combinations of their estimates,
This guarantees that linear combinations of integrals can be estimated by
linear combinations of their estimates,
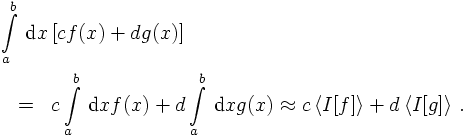
- There should be a family of functions h such that the residual term vanishes.
This translates into the median value to represent the exact value of the integral.
It can be shown that some weighted average fulfils both requirements; in other words,
M can be written as
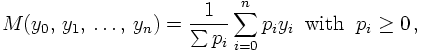 where the pi are the weights. In this definition, of course, there is some
freedom left, namely the number and distribution of sampling points xi
and the choice of the weights pi. This opens the possibility to try to
minimise the size of the residual term R in different ways. The most popular choice
is to use equidistant sampling points; for some finite interval [a,b] one therefore has
where the pi are the weights. In this definition, of course, there is some
freedom left, namely the number and distribution of sampling points xi
and the choice of the weights pi. This opens the possibility to try to
minimise the size of the residual term R in different ways. The most popular choice
is to use equidistant sampling points; for some finite interval [a,b] one therefore has
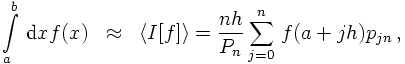 where
where
 In the table below, corresponding weights up to n=3 and an estimate of the residual term
are displayed.
In the table below, corresponding weights up to n=3 and an estimate of the residual term
are displayed.
| n | name |
p0n | p1n | p2n | p3n |
residual term |
| 1 | trapezoid |
1 | 1 | | |
 |
| 2 | Simpson |
1 | 4 | 1 | |
 |
| 2 | Newton 3/8 |
1 | 3 | 3 | 1 |
 |
Here, in all cases, &xi, is some arbitrary value inside the interval. However, for practical
purposes, i.e. for implementation in a computer code, this form of estimating the residual
term (and, thus, the error of the approximation) is of limited use only. There are a number
of methods to overcome this problem. The simplemost way is to iterate the procedure by
cutting the interval [a,b] in two halves and comparing the original estimator
<I[f]> over the full integral with the sum of the two estimators in the half-intervals.
If the difference is larger than some predefined error the procedure is repeated until
the result becomes stable.
It is clear that such a procedure is computationally intense and of limited use when going
to an increasing number of dimensions. This is because in such a case each partition
performed in all dimensions translates into multiplying the number of intervals by
2dim. Of course, smarter methods (e.g. selecting only those intervals for
partition, where the subresults are not yet stable) may reduce the computational cost of such
a quadrature somewhat. However, the basic idea of an exploding computational cost of
this approach remains.