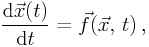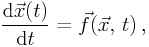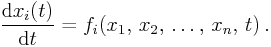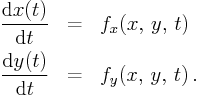Solving differential equations

Many typical problems in the physical sciences are described by ordinary differential equations of different order. A natural example is the motion of a particle under the influence of forces. Its trajectory can be written through time-dependent coordinates such as x(t), y(t) etc.. The presence of forces then implies that typically up to second derivatives of these coordinates enter the equation. It can be shown that such equations can be written as first-order differential equations, allowing us to use some of the techniques outlined below.
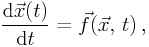These techniques typically aim at solving equations of the form Differential equations of order 1

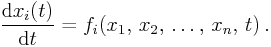or, in components, Differential equations of order 1

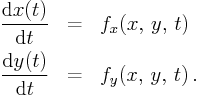Typically we will deal with 1- and 2-dimensional problems; the latter would thus lead to the system Differential equations of order 1

Here, obviously x_1,2 have been replaced by x and y, respectively. In the following some methods will be discussed to solve this type of equation numerically.

The Euler method and derivatives

The Euler method is the simplest method and relies on simple discretisation with uniform step size. For more details, read here.

Frank Krauss and Daniel Maitre

Last modified: Tue Oct 3 14:43:58 BST 2017