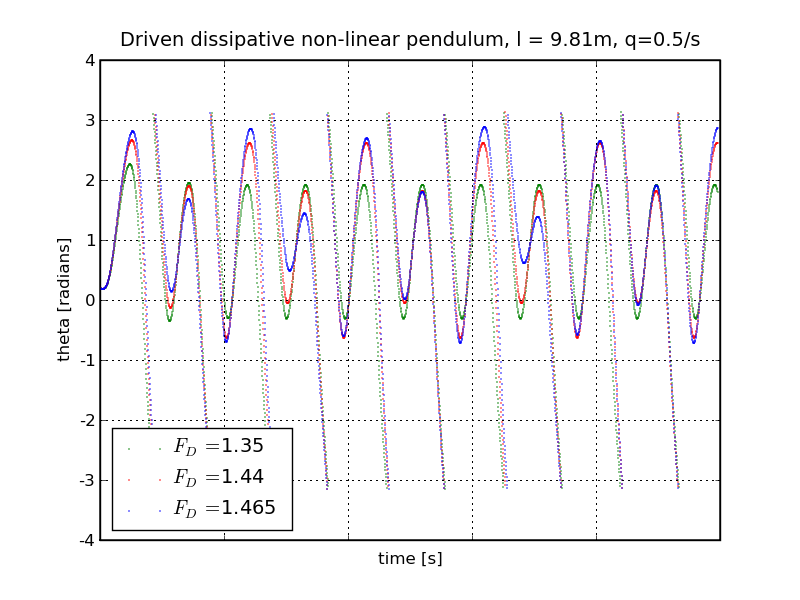
Up to now, we have seen two wildly different regimes for the driven non-linear pendulum, a chaotic and a non-chaotic one. It would be interesting to see how exactly the transition between the two regimes takes place. A careful study would reveal that for our pendulum with the length and dissipation as discussed so far, there is not only one transition somewhere between FD=0.5 and FD=1.2, but rather a chain of transitions. Since the first transition, the one between 0.5 and 1.2, is hard to study, we will now discuss larger values of the driving force. In the figure below, we show the time evolution of θ for different values of the driving force. Note that due to our choice of the driving frequency, the period of the driving force is 3π.

In our plot, at FD=1.35 (green), the pendulum, after "swinging in", moves with the same frequency as the driving force. This is nice, and somewhat less chaotic than we may have thought. But, interestingly, the next surprise is lurking around the corner: At FD=1.44 (red), the pendulum again exhibits periodic motion, but with twice the period. This can be seen by comparing the peak positions, which alternate in height. Things become even more interesting when considering FD=1.465 (blue), where we find four times the frequency. We can anticipate that this period doubling cascade would continue, if we raise the driving force further and further.
This surprise is an important one and central to driven chaotic systems: When a nonlinear system is excited or driven by a single frequency stimulus, in general the response is not confined to the same frequency; in contrast to linear systems, the response will contain harmonics like 2, 3, 4, ... times the driving frequency ΩD. This phenomenon is known as frequency mixing. It celebrates a standard appearsnce in many chaotic systems and it is well studied and well understood. What makes things really messy is that for our chaotic system also response frequencies of ΩD/2 etc. mix in, i.e. sub-harmonics.
Anyway, coming back to our period doubling (i.e. frequency halving - emergence of sub-harmonics), what about the transition to chaos. A nice way to see how this works is the bifurcation diagram below. (To see more on bifurcations, click here.) In this diagram we show values of θ at times that are in phase with the driving force, in dependence on the size of FD. We did so after waiting sufficiently long enough to allow the system to swing in.
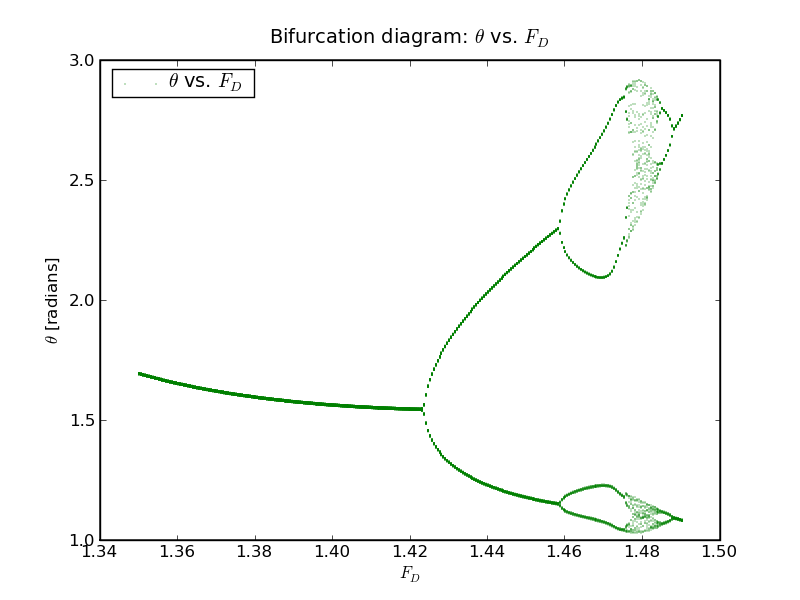
To understand this diagram, let us start to the left, at FD=1.35. There is only one single point, since the deflection angle and the driving force are parallel w.r.t. each other - they have the same period, as already noticed above. This remains the case, while we move to the right, towards larger driving force amplitudes. Until we hit around 1.43, we still have only one point, which, of course, is plotted multiple times in our plot. But then the first bifurcation happens, a period doubling takes place, and the deflection angle takes either of two values. The pattern becomes clear: Motion with period n times the driving period will lead to n points in the bifurcation diagram. This bifurcation repeats itself in a true cascade, where the distance between two bifurcation points on the FD axis becomes smaller and smaller. Ultimately, this ends in chaotic behaviour, and it is not clear any more where our pendulum is with respect to the driving force.
We have ultimately reached some qualitative understanding of the road to chaos, we understand in principle how it emerges for one particular system, our pendulum. A natural question to ask now is how general this behaviour is. Is it only found in the pendulum or are there other systems? If there are other systems, do they behave similarly, is there a pattern or do we do a stamp collection of unrelated phenomena? Or, in other words: Is the period-doubling road a universal feature? The answer given now is definitely not the last answer, we are still too far from an understanding of chaos that is as complete as the understanding of, for instance, electromagnetism in terms of Maxwell's laws. However, up to now, in the many systems with chaotic behaviour discovered so far, there are only few different roads to chaos, including period doubling as in our case at hand. And, yes, this pattern has some universality - there are other systems showing exactly the same behaviour.
But returning to our bifurcation diagram, we already noted that the distances between bifurcation points become smaller and smaller. If we define Fn as the value of the driving force amplitude FD at which a period doubling to 2n takes place and the bifurcation parameter δn through
then the observation of smaller distances implies δn>1. It has been found that for large n, δn approaches a constant δ, around 4.669, known as the Feigenbaum δ. It appears that all systems travelling the period doubling road as the way into chaos possess the same limit, a truly universal feature.